题目内容
已知E、F、G、H分别是空间四边形ABCD的边AB，BC，CD，DA的中点．
（1）证明E，F，G，H四点共面；
（2）证明BD∥平面EFGH．
（1）证明E，F，G，H四点共面；
（2）证明BD∥平面EFGH．
分析：（1）由向量加法法则得
=
（
+
），从而得到
=
+
=
+
（
+
），结合F是BC中点、EH是△ABD的中位线，可得
=
+
，从而得到得
、
、
是共面的向量，由此可得E、F、G、H四点共面；
（2）根据向量加法的三角形法则，结合三角形中位线定理得到
=2
+2
，从而向量
与
，
共面．再由BD是平面EFGH的殊一条直线，可得BD∥平面EFGH．
| BG |
| 1 |
| 2 |
| BC |
| BD |
| EG |
| EB |
| BG |
| EB |
| 1 |
| 2 |
| BC |
| BD |
| EG |
| EF |
| EH |
| EG |
| EF |
| EH |
（2）根据向量加法的三角形法则，结合三角形中位线定理得到
| BD |
| EG |
| GH |
| BD |
| EG |
| GH |
解答：解：如图，连结EG，BG．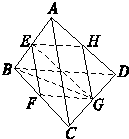
（1）∵BG是△BCD的中线，可得
=
（
+
）
∴
=
+
=
+
（
+
）
∵
=
，
=
∴
=
+
+
=
+
，
根据向量共面的充要条件，得
可得E，F，G，H四点共面．
（2）∵
=
+
，
=
+
∴
=
+
=2
+2
=2
=2（
+
）=2
+2
，
结合
，
不共线，可得
与
，
共面．
又∵BD?面EFGH，∴BD∥面EFGH．
（1）∵BG是△BCD的中线，可得
| BG |
| 1 |
| 2 |
| BC |
| BD |
∴
| EG |
| EB |
| BG |
| EB |
| 1 |
| 2 |
| BC |
| BD |
∵
| BF |
| 1 |
| 2 |
| BC |
| EH |
| 1 |
| 2 |
| BD |
∴
| EG |
| EB |
| BF |
| EH |
| EF |
| EH |
根据向量共面的充要条件，得
可得E，F，G，H四点共面．
（2）∵
| EH |
| EA |
| AH |
| EH |
| EG |
| GH |
∴
| BD |
| BA |
| AD |
| EA |
| AH |
| EH |
| EG |
| GH |
| EG |
| GH |
结合
| EG |
| GH |
| BD |
| EG |
| GH |
又∵BD?面EFGH，∴BD∥面EFGH．
点评：本题采用向量的线性运算的方法证明四点共面和线面平行．着重考查了三角形中位线定理、向量的加减法法则等知识，考查了向量共面与线面平行的关系，属于中档题．
练习册系列答案
教学练新同步练习系列答案
课前课后同步练习系列答案
相关题目
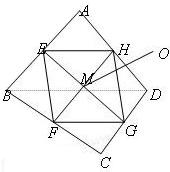已知E，F，G，H分别是空间四边形ABCD的边AB，BC，CD，DA的中点．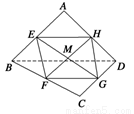
=
（
+
+
+
）.
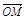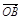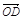