题目内容
设函数 .
.
(1)求 的最小正周期和值域;
的最小正周期和值域;
(2)在锐角△ 中,角
中,角 的对边分别为
的对边分别为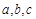 ,若
,若 且
且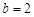 ,
,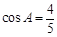 ,求
,求 和
和 .
.
(1)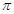 ,
,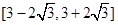 ;(2)
;(2)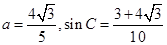 .
.
解析试题分析:(1)这是三角函数的典型问题,解决方法都是应用三角恒等式把它化为一个三角函数的形式: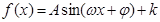 ,然后应用正弦函数的性质得出相应的结论;(2),由(1)
,然后应用正弦函数的性质得出相应的结论;(2),由(1)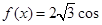

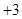 ,这样通过条件
,这样通过条件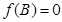 可求出
可求出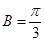 ,这样在
,这样在 中就相当于已知
中就相当于已知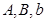 ,要求
,要求 ,显然应用正弦定理可得,而要求
,显然应用正弦定理可得,而要求 ,我们只要利用三角形的内角和为
,我们只要利用三角形的内角和为 ,由式子
,由式子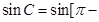
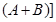
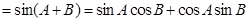 即可得.
即可得.
试题解析:(1)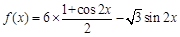 =
=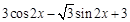
=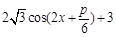 . 3分
. 3分
所以 的最小正周期为
的最小正周期为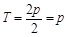 , 4分
, 4分
值域为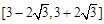 . 6分
. 6分
(2)由 ,得
,得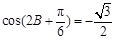 .
.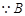 为锐角,∴
为锐角,∴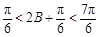 ,
,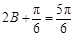 ,∴
,∴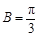 . 9分
. 9分
∵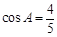 ,
,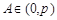 ,∴
,∴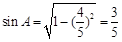 . 10分
. 10分
在△ABC中,由正弦定理得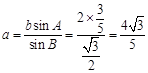 . 12分
. 12分
∴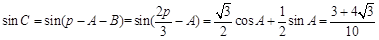 . 14分
. 14分
考点:(1)三角函数的性质;(2)解三角形.

练习册系列答案
 寒假大串联黄山书社系列答案
寒假大串联黄山书社系列答案 寒假创新型自主学习第三学期寒假衔接系列答案
寒假创新型自主学习第三学期寒假衔接系列答案
相关题目
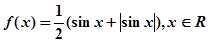
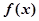 的周期T,与单调增区间.
的周期T,与单调增区间.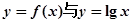 的图象有几个公共交点.
的图象有几个公共交点.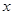 的函数
的函数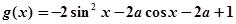 的最小值为
的最小值为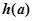 ,试确定满足
,试确定满足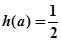 的
的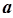 的值,并对此时的
的值,并对此时的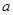 值求
值求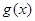 的最小值.
的最小值.
 的最大值,并写出
的最大值,并写出 时的取值集合;
时的取值集合; 中,角
中,角 的对边分别为
的对边分别为 ,若
,若 求
求 的最小值.
的最小值. ,且
,且 ,求
,求 的值。
的值。 ,
, .
. 的最小正周期;
的最小正周期; 、
、 ,
, ,
, ,求
,求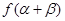 的值.
的值.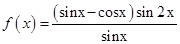 .
.  的定义域及最小正周期;
的定义域及最小正周期; )的部分图象如图所示.
)的部分图象如图所示.
 的单调递增区间.
的单调递增区间.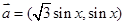 ,
,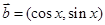 ,
,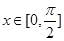
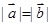 ,求
,求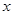 的值;
的值;  ,求
,求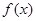 的最大值。
的最大值。 sinxcosx+cos2x+a.
sinxcosx+cos2x+a.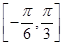 时,函数f(x)的最大值与最小值的和为
时,函数f(x)的最大值与最小值的和为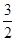 ,求a的值.
,求a的值.