题目内容
17.设a为实数,函数f(x)=(x2-a)e1-x.(Ⅰ)当x≥1时y=f(x)存在斜率为2的切线,求实数a的取值范围;
(Ⅱ)当f(x)有两个极值点x1,x2(x1<x2)时,是否存在实数λ,使x2f(x1)+aλ(e${\;}^{1-{x}_{1}}$+1)≤0?请说明你的理由.
分析 (Ⅰ)求出函数的导数,根据导函数的单调性求出a的范围即可;
(Ⅱ)问题转化为不等式x1[2${e}^{1{-x}_{1}}$-λ(${e}^{1{-x}_{1}}$+1)]≤0对任意x1∈(-∞,1)恒成立,通过讨论x1的范围结合函数的单调性求出满足条件的λ的值即可.
解答 解:(Ⅰ)f′(x)=(2x-x2+a)e1-x,
令f′(x)=(2x-x2+a)e1-x=2,得a=x2-2x+2ex-1,
令g(x)=x2-2x+2ex-1,(x≥1),
由于g(x)的导数g′(x)=2x-2+2ex-1≥2,
即g(x)在[1,+∞)递增,
故g(x)的最小值是g(1)=1,
故a的范围是[1,+∞);
(Ⅱ)由题意方程-x2+2x+a=0有2个不同的实数根x1,x2(不妨设x1<x2),
有-x2+2x+a=0,则△=4+4a>0,解得:a>-1,
且x1+x2=2,∵x1<x2,∴x1<1,
x2f(x1)+aλ(e${\;}^{1-{x}_{1}}$+1)≤0,
即(2-x1)(${{x}_{1}}^{2}$-a)${e}^{1{-x}_{1}}$≤λ[(2x1-${{x}_{1}}^{2}$)${e}^{1{-x}_{2}}$-a],
故(2-x1)(2x1)${e}^{1{-x}_{1}}$≤λ[(2x1-${{x}_{1}}^{2}$)${e}^{1{-x}_{2}}$+(2x1-${{x}_{1}}^{2}$)],
即不等式x1[2${e}^{1{-x}_{1}}$-λ(${e}^{1{-x}_{1}}$+1)]≤0对任意x1∈(-∞,1)恒成立,
①x1=0时,不等式x1[2${e}^{1{-x}_{1}}$-λ(${e}^{1{-x}_{1}}$+1)]≤0恒成立,λ∈R,
②x1∈(0,1)时,2${e}^{1{-x}_{1}}$-λ(${e}^{1{-x}_{1}}$+1)≤0,即λ≥$\frac{{2e}^{1{-x}_{1}}}{{e}^{1{-x}_{1}}+1}$,
令函数k(x)=$\frac{{2e}^{1-x}}{{e}^{1-x}+1}$=2-$\frac{2}{{e}^{1-x}+1}$,
显然k′(x)=-$\frac{{2e}^{1-x}}{{(1{+e}^{1-x})}^{2}}$<0,k(x)在R递减,
∴当x∈(0,1)时,k(x)<k(0)=$\frac{2e}{e+1}$,
∴λ≥$\frac{2e}{e+1}$;
③x1∈(-∞,0)时,2${e}^{1{-x}_{1}}$-λ(${e}^{1{-x}_{1}}$+1)≥0恒成立,
即λ≤$\frac{{2}^{1{-x}_{1}}}{{e}^{1{-x}_{1}}+1}$,
由②得x∈(-∞,0)时,k(x)>k(0)=$\frac{2e}{e+1}$,即λ≤$\frac{2e}{e+1}$,
综上,存在λ=$\frac{2e}{e+1}$使得x2f(x1)+aλ(e${\;}^{1-{x}_{1}}$+1)≤0总成立.
点评 本题考查了函数的单调性、最值问题,考查导数的应用以及分类讨论思想、转化思想,是一道综合题.

 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案| A. | 2015 | B. | 2016 | C. | 2017 | D. | 2018 |
| A. | 8068 | B. | 2017 | C. | -8027 | D. | -2013 |
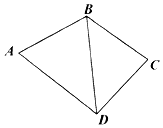 四边形ABCD如图所示,已知AB=BC=CD=2,AD=2$\sqrt{3}$.
四边形ABCD如图所示,已知AB=BC=CD=2,AD=2$\sqrt{3}$.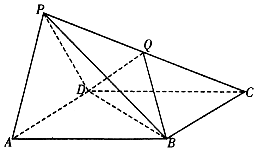 如图,四棱锥P-ABCD的底面ABCD是平行四边形,侧面PAD是边长为2的正三角形,AB=BD=$\sqrt{7}$,PB=3.
如图,四棱锥P-ABCD的底面ABCD是平行四边形,侧面PAD是边长为2的正三角形,AB=BD=$\sqrt{7}$,PB=3.