题目内容

已知a、b是夹角为60°的两个单位向量，而向量c⊥a,c⊥b,且|c|=,x=2a-b+c,y=3b-a-c,则cos〈x,y〉=_____________.

答案:

解析:∵c⊥a,c⊥b,

∴a·c=0,b·c=0.

又∵x·y=(2a-b+c)·(3b-a-c)=6a·b-2a2-2a·c-3b2+a·b+b·c+3b·c-a·c-c2=6·-2-3+-3=-,

|x|2=(2a-b+c)2=4a2+b2+c2-4a·b+4a·c-2b·c=4+1+3-4·=6,

∴|x|=6,

|y|2=(3b-a-c)2=a2+9b2+c2-6a·b-6b·c+2a·c=1+9+3-6·=10.

∴|y|=10.

∴cos〈x,y〉==.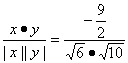


练习册系列答案
相关题目
给出下列四个命题：
①如果命题“?p”与命题“p或q”都是真命题，那么命题q一定是真命题；
②已知向量
a
，
b
满足|
a
|=1，|
b
|=4，且
a
•
b
=2，则
a
与
b
的夹角为
π
6
；
③若函数f（x+1）是奇函数，f（x-1）是偶函数，且f（0）=2，则f（2012）=2；
④已知函数f(x)=log4(4x+1)+kx(k∈R)是偶函数，函数g(x)=log4(a•2x-
4
3
a)，若函数f（x）的图象与函数g（x）的图象有且只有一个公共点，则实数a的取值范围是（1，+∞）．
其中正确命题的序号为
①
①
．
已知
a
，
b
是两个非零向量，且|
a
|=|
b
|=|
a
-
b
|，则
a
与
a
+
b
的夹角大小为
π
6
π
6
．
已知向量
a
，
b
，
c
满足|
a|
=2，|
b
|=|
a
-
b
|，
a
与
b
的夹角为
π
6
，(
a
-
c
)•(
b
-
c
)=0．若对每一个确定的
b
，|
c
|的最大值和最小值分别为m，n，则对任何的
b
，m-n的最小值是（　　）
给出下列四个命题：
①如果命题“?p”与命题“p或q”都是真命题，那么命题q一定是真命题；
②已知向量
a
，
b
满足|
a
|=1，|
b
|=4，且
a
•
b
=2，则
a
与
b
的夹角为
π
6
；
③若函数f（x+1）是奇函数，f（x-1）是偶函数，且f（0）=2，则f（2012）=2；
④已知函数f(x)=log4(4x+1)+kx(k∈R)是偶函数，函数g(x)=log4(a•2x-
4
3
a)，若函数f（x）的图象与函数g（x）的图象有且只有一个公共点，则实数a的取值范围是（1，+∞）．
其中正确命题的序号为______．
已知向量
a
，
b
，
c
满足|
a|
=2，|
b
|=|
a
-
b
|，
a
与
b
的夹角为
π
6
，(
a
-
c
)•(
b
-
c
)=0．若对每一个确定的
b
，|
c
|的最大值和最小值分别为m，n，则对任何的
b
，m-n的最小值是（　　）
A．
1
4
B．
1
2
C．2D．1

违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com

精英家教网