题目内容
20.已知点M,N分别是空间四面体OABC的边OA和BC的中点,P为线段MN的中点,若$\overrightarrow{OP}=λ\overrightarrow{OA}+μ\overrightarrow{OB}+γ\overrightarrow{OC}$,则实数λ+μ+γ=$\frac{3}{4}$.分析 要充分利用图形的直观性,熟练利用向量加法的三角形法则进行运算.
解答 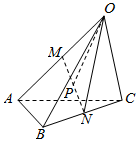 解:如图,连接ON,在△OMN中,点P是MN中点,
解:如图,连接ON,在△OMN中,点P是MN中点,
则由平行四边形法则得$\overrightarrow{OP}$=$\frac{1}{2}$($\overrightarrow{OM}$+$\overrightarrow{ON}$)
=$\frac{1}{2}$$\overrightarrow{OM}$+$\frac{1}{2}$$\overrightarrow{ON}$=$\frac{1}{4}$$\overrightarrow{OA}$+$\frac{1}{2}$•$\frac{1}{2}$($\overrightarrow{OB}$+$\overrightarrow{OC}$)
=$\frac{1}{4}$$\overrightarrow{OA}$+$\frac{1}{4}$$\overrightarrow{OB}$+$\frac{1}{4}$$\overrightarrow{OC}$,
∴λ+μ+γ=$\frac{3}{4}$,
故答案为:$\frac{3}{4}$.
点评 本题考查空间向量的运算,即向量加法的平行四边形法则,三角形法则,空间向量基基底的概念,空间向量的基本定理及其意义.

练习册系列答案
 愉快的寒假南京出版社系列答案
愉快的寒假南京出版社系列答案
相关题目
5.抛物线的准线方程是y=-1,则抛物线的标准方程是( )
| A. | x2=4y | B. | x2=-4y | C. | y2=4x | D. | y2=-4x |
9.下列函数中,是奇函数且在(0,1]上单调递减的函数是( )
| A. | y=-x2+2x | B. | y=x+$\frac{1}{x}$ | C. | y=2x-2-x | D. | y=1-$\sqrt{x}$ |
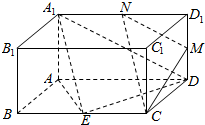 如图,长方体ABCD-A1B1C1D1中,AA1=AB=1,AD=2,E为BC的中点,点M,N分别为棱DD1,A1D1的中点.
如图,长方体ABCD-A1B1C1D1中,AA1=AB=1,AD=2,E为BC的中点,点M,N分别为棱DD1,A1D1的中点.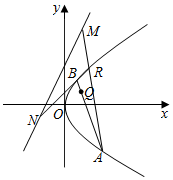 已知抛物线C的方程为y2=2px(p>0),抛物线的焦点到直线l:y=2x+2的距离为$\frac{4\sqrt{5}}{5}$.
已知抛物线C的方程为y2=2px(p>0),抛物线的焦点到直线l:y=2x+2的距离为$\frac{4\sqrt{5}}{5}$.