题目内容
若不等式x2+bx+c＜0的解集是（-1，2），则b+c=________．
-3
分析：方程x2+bx+c=0的两根为 x1=-1，x2=2，利用根与系数的关系列方程组解得b和c的值，从而求得b+c．
解答：由题意知，方程x2+bx+c=0的两根为 x1=-1，x2=2，
又
，即 
，解得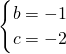 
，
∴b+c=-3．
故答案为：-3．
点评：此题是基础题．本题考查一元二次不等式的解法，一元二次方程根与系数的关系，注意方程的根与不等式解集之间的关系，体现了转化的思想．
分析：方程x2+bx+c=0的两根为 x1=-1，x2=2，利用根与系数的关系列方程组解得b和c的值，从而求得b+c．
解答：由题意知，方程x2+bx+c=0的两根为 x1=-1，x2=2，
又
，即 ，解得 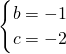，∴b+c=-3．
故答案为：-3．
点评：此题是基础题．本题考查一元二次不等式的解法，一元二次方程根与系数的关系，注意方程的根与不等式解集之间的关系，体现了转化的思想．
练习册系列答案
名校课堂系列答案
相关题目