题目内容
3.等差数列{an}的前n项和为Sn,且满足a4=9,a3+a7=22.(1)求an和Sn;
(2)设${b_n}=\frac{1}{{{a_n}{a_{n+1}}}}$,求数列{bn}的前n项和Tn.
分析 (1)利用等差数列的通项公式与求和公式及其性质即可得出.
(2)利用“裂项求和”方法即可得出.
解答 解:(1)a3+a7=22=2a5,∴a5=11.
∴公差d=11-9=2,a1+3d=9,解得a1=3.
∴an=2n+1,
${S_n}=\frac{n(3+2n+1)}{2}={n^2}+2n$.
(2)${b_n}=\frac{1}{(2n+1)(2n+3)}$${b_n}=\frac{1}{2}({\frac{1}{2n+1}-\frac{1}{2n+3}})$,
∴${T_n}=\frac{1}{2}({\frac{1}{3}-\frac{1}{2n+3}})=\frac{n}{3(2n+3)}$.
点评 本题考查了等差数列的通项公式与求和公式及其性质,考查了推理能力与计算能力,属于中档题.

练习册系列答案
相关题目
14.已知函数f(x)满足下列条件:①定义域为[1,+∞);②当1<x≤2时f(x)=4sin($\frac{π}{2}$x);③f(x)=2f(2x).若关于x的方程f(x)-kx+k=0恰有3个实数解,则实数k的取值范围是( )
| A. | $[\frac{1}{14},\frac{1}{3})$ | B. | $(\frac{1}{14},\frac{1}{3}]$ | C. | $(\frac{1}{3},2]$ | D. | $[\frac{1}{3},2)$ |
18.已知函数$f(x)=\left\{\begin{array}{l}{e^x}+m\;-1,x≥0\\ ax+b,x<0\end{array}\right.$其中m<-1,对于任意x1∈R且x1≠0,均存在唯一实数x2,使得f(x2)=f(x1),且x1≠x2,若|f(x)|=f(m)有4个不相等的实数根,则a的取值范围是( )
| A. | (0,1) | B. | (-1,0) | C. | (-2,-1)∪(-1,0) | D. | (-2,-1) |
8.21个人按照以下规则表演节目:他们围坐一圈,按顺序从1到3循环报数,报数字“3”的人出来表演节目,并且表演过的人不再参加报数,那么在仅剩两个人没有表演过节目的时候,共报数的次数为( )
| A. | 19 | B. | 38 | C. | 51 | D. | 64 |
15.在平面直角坐标系中,角α的终边经过点(-$\frac{1}{2}$,$\frac{\sqrt{3}}{2}$),则sinα的值为( )
| A. | $\frac{1}{2}$ | B. | -$\frac{1}{2}$ | C. | -$\frac{\sqrt{3}}{2}$ | D. | $\frac{\sqrt{3}}{2}$ |
12.某手机厂商推出一次智能手机,现对500名该手机使用者(200名女性,300名男性)进行调查,对手机进行打分,打分的频数分布表如下:
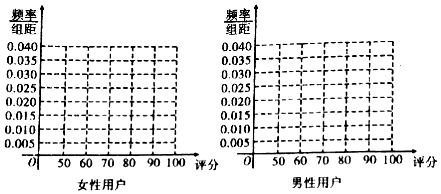
(1)完成下列频率分布直方图,并比较女性用户和男性用户评分的方差大小(不计算具体值,给出结论即可);
(2)根据评分的不同,运用分层抽样从男性用户中抽取20名用户,在这20名用户中,从评分不低于80分的用户中任意取2名用户,求2名用户评分小于90分的概率.

| 女性用户 | 分值区间 | [50,60) | [60,70) | [70,80) | [80,90) | [90,100) |
| 频数 | 20 | 40 | 80 | 50 | 10 | |
| 男性用户 | 分值区间 | [50,60) | [60,70) | [70,80) | [80,90) | [90,100) |
| 频数 | 45 | 75 | 90 | 60 | 30 |
(2)根据评分的不同,运用分层抽样从男性用户中抽取20名用户,在这20名用户中,从评分不低于80分的用户中任意取2名用户,求2名用户评分小于90分的概率.
