题目内容
已知向量 ,
, 夹角为
夹角为 ,且|
,且| |=1,|
|=1,| |=
|= ,则|
,则| |等于( )
|等于( )
A. | B. | C. | D. |
C
解析试题分析:本题是对向量数量积的考查,根据两个向量的夹角和模之间的关系,用数量积列出等式,再根据和的模两边平方,联立解题,注意要求的结果非负,舍去不合题意的即可.根据向量 ,
, 夹角为
夹角为 ,且|
,且| |=1,|
|=1,| |=
|= ,那么两边平方,得到4+
,那么两边平方,得到4+ ,|
,| |等于
|等于 ,选C
,选C
考点:向量的数量积
点评:两个向量的数量积是一个数量,它的值是两个向量的模与两向量夹角余弦的乘积,结果可正、可负、可以为零,其符号由夹角的余弦值确定.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
平面四边形ABCD中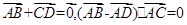 ,则四边形ABCD是( )
,则四边形ABCD是( )
| A.矩形 | B.正方形 | C.菱形 | D.梯形 |
已知向量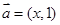 ,
,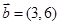 ,且
,且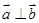 ,则实数
,则实数 的值为( )
的值为( )
A. | B.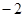 | C.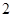 | D.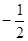 |
向量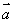 与
与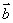 的夹角为
的夹角为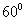 ,
,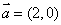 ,
,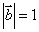 则
则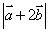 =( )
=( )
A.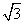 | B.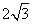 | C.4 | D.12 |
已知向量 ,向量
,向量 ,且
,且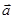 与
与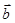 的夹角为
的夹角为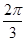 ,则
,则 在
在 方向上的投影是( )
方向上的投影是( )
A.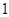 | B.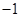 | C.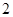 | D.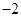 |
设 、
、 、
、 为同平面内具有相同起点的任意三个非零向量,且满足
为同平面内具有相同起点的任意三个非零向量,且满足 与
与 不共线,
不共线, ,
, ,则
,则 的值一定等于( )
的值一定等于( )
A.以 、 、 为两边的三角形面积; 为两边的三角形面积; | B.以 、 、 为邻边的平行四边形的面积; 为邻边的平行四边形的面积; |
C.以 、 、 为两边的三角形面积; 为两边的三角形面积; | D.以 、 、 为邻边的平行四边形的面积. 为邻边的平行四边形的面积. |
已知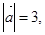
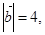
 则
则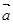 与
与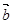 的夹角为 ( )
的夹角为 ( )
A.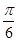 | B.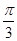 | C.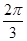 | D. |
设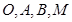 为平面上四点,
为平面上四点,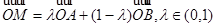 ,则
,则
A.点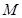 在线段 在线段 上 上 | B.点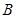 在线段 在线段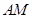 上 上 |
C.点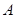 在线段 在线段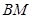 上 上 | D.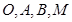 四点共线 四点共线 |

