题目内容

12．在△ABC中，A=$\frac{π}{4}$，b2sinC=$4\sqrt{2}$sinB，则△ABC的面积为2．

分析 利用正弦定理将角化边得到bc=4$\sqrt{2}$，代入面积公式即可求出．

解答 解：∵b2sinC=$4\sqrt{2}$sinB，∴b2c=4$\sqrt{2}$b，即bc=4$\sqrt{2}$．
∴S△ABC=$\frac{1}{2}$bcsinA=$\frac{1}{2}×4\sqrt{2}×\frac{\sqrt{2}}{2}$=2．
故答案为：2．

点评 本题考查了正弦定理得应用，属于基础题．

练习册系列答案
相关题目
2．已知函数f（x）=x3-$\frac{1}{2}$x2+bx+c，若f（x）在R上是增加的，求实数b的最小值．
3．已知椭圆C：$\frac{{x}^{2}}{{a}^{2}}+\frac{{y}^{2}}{{b}^{2}}=1$（a＞b＞0）的离心率为$\frac{\sqrt{3}}{2}$，且点（$\sqrt{2}$，$\frac{\sqrt{2}}{2}$）在C上．
（1）求椭圆C的方程；
（2）直线l经过点P（1，0），且与椭圆C有两个交点A，B，是否存在直线l0：x=x0（其中x0＞2），问A，B到l0的距离dA，dB满足：$\frac{{d}_{A}}{{d}_{B}}$=$\frac{|PA|}{|PB|}$恒成立？若存在，求x0的值；若不存在，请说明理由．
20．已知函数f（x）=x-alnx+$\frac{1-a}{x}$（a∈R），g（x）=x-1．
（Ⅰ）若函数f（x）在x=2处取得极值，求实数a的值；
（Ⅱ）是否存在a∈（3，+∞），对任意x1$∈[\frac{1}{e}，1]$，总存在x2$∈[\frac{1}{e}，1]$，使得g（x1）=f（x2）成立．若存在，求出a的范围；若不存在，请说明理由．
7．现今新开发的一种自控系统，可以在一定的程度上帮助人们解决刹车的问题，避免了很多的危险发生，假设在某种路面上的刹车距离s（米）与汽车的速度x（千米/小时）之间有如下关系：s=$\frac{1}{80}$x+$\frac{1}{160}$x2，在一次前方有人，刹车自动开启后，在离人1米处汽车刹车成功，测得这种汽车的刹车距离小于15米．问这辆车刹车时的车速最大为多少？
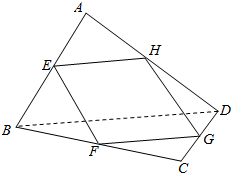17．已知：空间四边形ABCD中，E、F、G、H分别为AB、BC、CD、DA的中点．求证：E、F、G、H四点共面（如图所示）
4．已知$\frac{（x+2i）-（1-yi）}{2-i}$=1+i，则实数x=4，y=-1．
1．已知公差大于零的等差数列{an}的前n项和为Sn，且满足a3a4=117，a2+a5=22．
（1）求{an}的通项公式．
（2）等差数列{bn}的通项公式为bn=$\frac{{S}_{n}}{n+c}$，求非零常数c的值．
2．已知函数f（x）=lnx，g（x）=x2-2ax+1，a∈R．
（Ⅰ）设函数h（x）=af（x）+g（x），若h（x）在区间（$\frac{1}{2}$，1）上是增函数，求实数a的取值范围．
（Ⅱ）设函数F（x）=f（x）+g（x），若对任意a$∈（1，\sqrt{2}$），都存在x0∈（0，1]，使得不等式F（x0）＞m（a-a2）-lna成立，求实数m的最小值．

违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com

精英家教网