题目内容
(本小题满分12分)已知函数 ,
,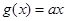 ,
,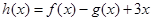 ,其中
,其中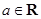 且
且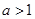 .
.
(I)求函数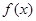 的导函数
的导函数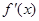 的最小值;
的最小值;
(II)当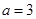 时,求函数
时,求函数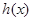 的单调区间及极值;
的单调区间及极值;
(III)若对任意的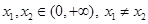 ,函数
,函数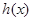 满足
满足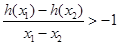 ,求实数
,求实数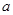 的取值范围.
的取值范围.
 ,
,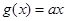 ,
,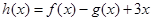 ,其中
,其中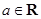 且
且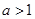 .
.(I)求函数
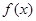 的导函数
的导函数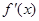 的最小值;
的最小值;(II)当
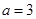 时,求函数
时,求函数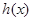 的单调区间及极值;
的单调区间及极值;(III)若对任意的
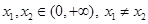 ,函数
,函数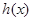 满足
满足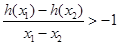 ,求实数
,求实数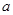 的取值范围.
的取值范围.(I)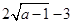 ;(II)单调增区间是
;(II)单调增区间是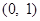 ,
, ;单调减区间是
;单调减区间是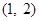 ;
;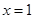 处取得极大值
处取得极大值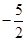 ,在
,在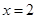 处取得极小值
处取得极小值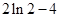 .(III)
.(III)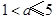 。
。
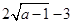 ;(II)单调增区间是
;(II)单调增区间是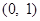 ,
, ;单调减区间是
;单调减区间是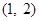 ;
;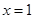 处取得极大值
处取得极大值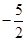 ,在
,在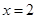 处取得极小值
处取得极小值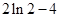 .(III)
.(III)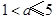 。
。试题分析:(I)
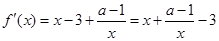 ,其中
,其中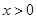 .
.因为
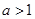 ,所以
,所以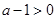 ,又
,又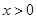 ,所以
,所以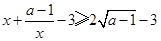 ,
,当且仅当
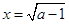 时取等号,其最小值为
时取等号,其最小值为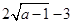 . 2……………………4分
. 2……………………4分(II)当
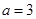 时,
时,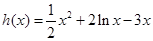 ,
,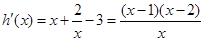 .…5分
.…5分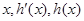 的变化如下表:
的变化如下表: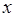 | 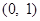 | 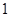 | 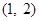 | 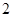 |  |
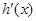 | 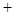 | 0 | 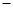 | 0 | 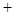 |
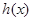 |  | 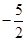 |  | 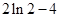 |  |
所以,函数
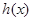 的单调增区间是
的单调增区间是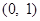 ,
, ;单调减区间是
;单调减区间是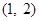 .……7分
.……7分函数
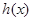 在
在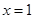 处取得极大值
处取得极大值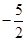 ,在
,在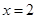 处取得极小值
处取得极小值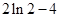 .……8分
.……8分(III)由题意,
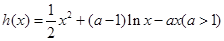 .
.不妨设
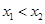 ,则由
,则由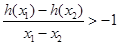 得
得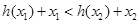 .
. 令
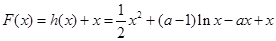 ,则函数
,则函数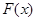 在
在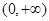 单调递增.10分
单调递增.10分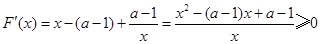 在
在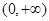 恒成立.
恒成立.即
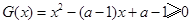 在
在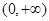 恒成立.
恒成立.因为
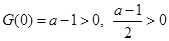 ,因此,只需
,因此,只需 .
.解得
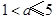 . 故所求实数
. 故所求实数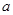 的取值范围为
的取值范围为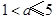 . …12分
. …12分点评:构造出函数
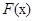 ,把证明
,把证明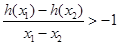 转化为证明
转化为证明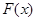 在
在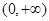 单调递增是做本题的关键,运用了转化思想,对学生的能力要求较高,是一道中档题。
单调递增是做本题的关键,运用了转化思想,对学生的能力要求较高,是一道中档题。
练习册系列答案
 走进文言文系列答案
走进文言文系列答案
相关题目
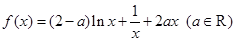 .
.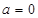 时,求
时,求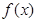 的极值;
的极值;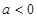 时,求
时,求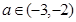 及
及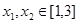 ,恒有
,恒有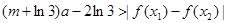 成立,求
成立,求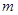 的取值范围
的取值范围
 的单调区间和极值;
的单调区间和极值; 的图象与函数
的图象与函数 的图象关于直线
的图象关于直线 对称,证明:当
对称,证明:当 时,
时, ;
; 且
且 ,证明:
,证明:
 在(1,4)上是减函数,则实数
在(1,4)上是减函数,则实数 的取值范围是( )
的取值范围是( )



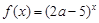 是R上的减函数;命题q:在
是R上的减函数;命题q:在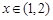 时,不等式
时,不等式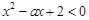 恒成立,若p∪q是真命题,求实数a的取值范围.
恒成立,若p∪q是真命题,求实数a的取值范围. 。
。 ,而使得不等式
,而使得不等式 能成立,求实数
能成立,求实数 的最小值;
的最小值; 在区间
在区间 上恰有两个不同的零点,求实数
上恰有两个不同的零点,求实数 的取值范围。
的取值范围。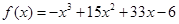 的单调增区间为 .
的单调增区间为 .
 的表达式(不需证明);
的表达式(不需证明); 的最大值为
的最大值为 ,
, ,求
,求 的最小值.
的最小值.