题目内容
已知等差数列an的首项为2,第10项为1,记Pn=a2+a4+…+a2n,(n∈N),求数列Pn中的最大项,并指出最大项使该数列中的第几项.
设公差为d
∵a1=2,a10=1
∴d=
=-
∴a2n=a1+(2n-1)(-
)=
-
2n
令
-
2n≥0得n≤4
∴P4最大P4=Pn=a2+a4+a8+a16=
-
+
-
+
-
+
-
=
故数列Pn中的最大项为
,是该数列中的第4项.
∵a1=2,a10=1
∴d=
| a10-a1 |
| 10-1 |
| 1 |
| 9 |
∴a2n=a1+(2n-1)(-
| 1 |
| 9 |
| 19 |
| 9 |
| 1 |
| 9 |
令
| 19 |
| 9 |
| 1 |
| 9 |
∴P4最大P4=Pn=a2+a4+a8+a16=
| 19 |
| 9 |
| 2 |
| 9 |
| 19 |
| 9 |
| 4 |
| 9 |
| 19 |
| 9 |
| 8 |
| 9 |
| 19 |
| 9 |
| 16 |
| 9 |
| 46 |
| 9 |
故数列Pn中的最大项为
| 46 |
| 9 |

练习册系列答案
 举一反三同步巧讲精练系列答案
举一反三同步巧讲精练系列答案 口算与应用题卡系列答案
口算与应用题卡系列答案 名师点睛字词句段篇系列答案
名师点睛字词句段篇系列答案
相关题目
 项和为
项和为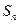 ,且它的第4项与第8项之和等与
,且它的第4项与第8项之和等与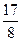 ,第5项与第7项之积等与
,第5项与第7项之积等与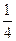 ,则
,则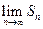 =________。
=________。