题目内容
在等比数列{an}中,a1+an=66,a2an-1=128,Sn=126,则n的值为( )
| A.5 | B.6 | C.7 | D.8 |
由题意可得a1+an=66,a1 •an =a2an-1=128,根据韦达定理推知a1和an是方程x2-66x+128=0的两根,
∴a1=2且 an=64,故 qn-1=32; 或a1=64 且an=2,故 qn-1=
.
当 a1=2 且 an=64,qn-1=32 时,再由Sn=126=
,求得q=2,∴n=6.
当 a1=64 且an=2,qn-1=
时,再由Sn=126=
,求得q=
,∴n=6.
综上可得,n=6,
故选B.
∴a1=2且 an=64,故 qn-1=32; 或a1=64 且an=2,故 qn-1=
| 1 |
| 32 |
当 a1=2 且 an=64,qn-1=32 时,再由Sn=126=
| a1(1-qn) |
| 1-q |
当 a1=64 且an=2,qn-1=
| 1 |
| 32 |
| a1(1-qn) |
| 1-q |
| 1 |
| 2 |
综上可得,n=6,
故选B.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
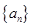 的前
的前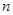 项和为
项和为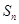 ,且
,且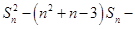
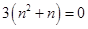 ,
,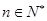 .
.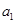 的值;
的值;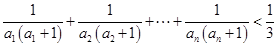 .
.