题目内容
下列说法中,正确的是 .
①任取x>0,均有3x>2x.
②当a>0,且a≠1时,有a3>a2.
③y=(
)-x是增函数.
④y=2|x|的最小值为1.
⑤在同一坐标系中,y=2x与y=2-x的图象关于y轴对称.
①任取x>0,均有3x>2x.
②当a>0,且a≠1时,有a3>a2.
③y=(
| 3 |
④y=2|x|的最小值为1.
⑤在同一坐标系中,y=2x与y=2-x的图象关于y轴对称.
考点:命题的真假判断与应用
专题:函数的性质及应用
分析:①运用幂函数的单调性,即可判断;
②运用指数函数的单调性,注意讨论a的范围,即可判断;
③由指数函数的单调性,即可判断;
④由|x|≥0,结合指数函数的单调性,即可判断;
⑤由指数函数的图象和关于y轴对称的特点,即可判断.
②运用指数函数的单调性,注意讨论a的范围,即可判断;
③由指数函数的单调性,即可判断;
④由|x|≥0,结合指数函数的单调性,即可判断;
⑤由指数函数的图象和关于y轴对称的特点,即可判断.
解答:
解:①任取x>0,则由幂函数的单调性:幂指数大于0,函数值在第一象限随着x的增大而增大,
可得,均有3x>2x.故①对;
②运用指数函数的单调性,可知a>1时,a3>a2,0<a<1时,a3<a2.故②错;
③y=(
)-x即y=(
)x,由于0<
<1,故函数是减函数.故③错;
④由于|x|≥0,可得2|x|≥20=1,故y=2|x|的最小值为1.故④对;
⑤由关于y轴对称的特点,可得:在同一坐标系中,y=2x与y=2-x的图象关于y轴对称,故⑤对.
故答案为:①④⑤.
可得,均有3x>2x.故①对;
②运用指数函数的单调性,可知a>1时,a3>a2,0<a<1时,a3<a2.故②错;
③y=(
| 3 |
| ||
| 3 |
| ||
| 3 |
④由于|x|≥0,可得2|x|≥20=1,故y=2|x|的最小值为1.故④对;
⑤由关于y轴对称的特点,可得:在同一坐标系中,y=2x与y=2-x的图象关于y轴对称,故⑤对.
故答案为:①④⑤.
点评:本题考查函数的性质和运用,考查函数的单调性、最值和图象的对称性,属于基础题.

练习册系列答案
相关题目
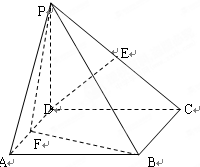 如图,四棱锥P-ABCD中,四边形ABCD为正方形,PD⊥面ABCD,PD=DA=2,F,E分别为AD,PC的中点.
如图,四棱锥P-ABCD中,四边形ABCD为正方形,PD⊥面ABCD,PD=DA=2,F,E分别为AD,PC的中点.