题目内容
已知在△ABC中,角A,B,C的对边分别是a,b,c,满足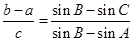 ,关于x的不等式x2cosC+4xsinC+6≥0对任意的x∈R恒成立.
,关于x的不等式x2cosC+4xsinC+6≥0对任意的x∈R恒成立.
(1)求角A的值;
(2)求f(C)=2sinC·cosB的值域.
(1)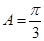 ;(2)
;(2)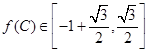 .
.
解析试题分析:本题主要考查解三角形中的正弦定理、余弦定理的应用、两角和与差的三角公式、函数的值域等数学知识,考查学生灵活运用数学公式的能力、转化能力以及计算能力.第一问,先利用正弦定理将角化为边,它类似于余弦定理的公式,再利用余弦定理求出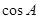 ,利用三角函数值在
,利用三角函数值在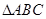 内求角,由于
内求角,由于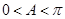 ,而
,而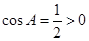 ,所以A为锐角;第二问,因为
,所以A为锐角;第二问,因为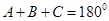 ,所以
,所以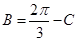 ,代入到解析式中,利用两角和与差的正余弦公式化简表达式,由于关于x的不等式x2cosC+4xsinC+6≥0对任意的x∈R恒成立,所以
,代入到解析式中,利用两角和与差的正余弦公式化简表达式,由于关于x的不等式x2cosC+4xsinC+6≥0对任意的x∈R恒成立,所以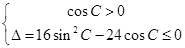 ,解出
,解出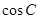 的取值范围,在
的取值范围,在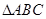 中解出角C的取值范围,将得到的角C的范围代入到
中解出角C的取值范围,将得到的角C的范围代入到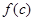 解析式中,求函数值域.
解析式中,求函数值域.
试题解析:(1)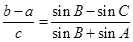
由正弦定理、余弦定理得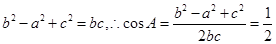 ,
,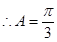 ,………6分
,………6分
(2)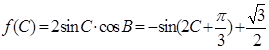 ,
,
∵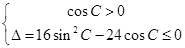
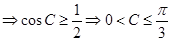
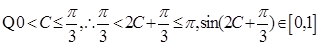
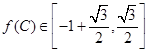 …12分
…12分
考点:1.正弦定理;2.余弦定理;3.两角和与差的正弦、余弦公式;4.函数值域.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
 、
、 、
、 为
为 的三内角,且其对边分别为
的三内角,且其对边分别为 、
、 、
、 ,若
,若 .
. ,求
,求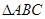 中,角
中,角 、
、 、
、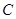 所对的边分别为
所对的边分别为 、
、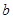 、
、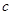 .已知
.已知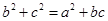 .
.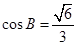 ,
, ,求
,求 中,角
中,角 ,
, ,
, 所对的边分别是
所对的边分别是 ,
, ,
, ,且满足
,且满足 .
. 的最大值,并求取得最大值时角
的最大值,并求取得最大值时角 的大小.
的大小. ,相距10海里C处的乙船,乙船当即决定匀速前往救援,并且与甲船同时到达。(供参考使用:
,相距10海里C处的乙船,乙船当即决定匀速前往救援,并且与甲船同时到达。(供参考使用: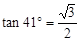 ).
).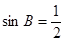 .
.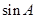 和
和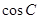 的值;
的值;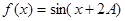 ,求
,求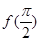 的值.
的值.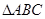 的内角
的内角 所对的边分别为
所对的边分别为 ,且有
,且有 .
. 的值;
的值; ,
, ,
,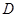 为
为 上一点.且
上一点.且 ,求
,求 的长.
的长.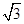 sin x,1),n=(cos x,-y),且m⊥n.
sin x,1),n=(cos x,-y),且m⊥n. =3,且a=2,b+c=4,求△ABC的面积.
=3,且a=2,b+c=4,求△ABC的面积.