题目内容
设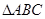 的内角
的内角 所对的边分别为
所对的边分别为 ,且有
,且有 .
.
(1)求 的值;
的值;
(2)若 ,
, ,
,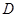 为
为 上一点.且
上一点.且 ,求
,求 的长.
的长.
(1) ;(2)
;(2) .
.
解析试题分析:(1)由 ,首先对其进行切割化弦,得到
,首先对其进行切割化弦,得到 ,去分母,化为整式,利用两角和与差的三角函数公式化简,再利用三角形内角和为
,去分母,化为整式,利用两角和与差的三角函数公式化简,再利用三角形内角和为 ,利用诱导公式即可求出
,利用诱导公式即可求出 的值;(2)求
的值;(2)求 的长,由
的长,由 ,
, ,
, ,利用余弦定理可求出
,利用余弦定理可求出 的值,发现
的值,发现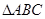 是等腰三角形,从而得
是等腰三角形,从而得 ,再由
,再由 ,可求得
,可求得 ,在
,在 中利用余弦定理可求出
中利用余弦定理可求出 的长.
的长.
试题解析:(1)∵  ∴
∴
∴ 
∵ ∴
∴ ∴
∴  .6分
.6分
(2)∵  ,
, ∴
∴  ∴
∴  ,
, 
∴ ∴
∴ 12分
12分
考点:解三角形.

练习册系列答案
相关题目
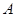 到
到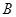 ,方位角(从正北方向顺时针转到
,方位角(从正北方向顺时针转到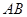 方向所成的角)是
方向所成的角)是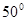 ,距离是3km;从
,距离是3km;从 ,方位角是110°,距离是3km;从
,方位角是110°,距离是3km;从 ,方位角是140°,距离是(
,方位角是140°,距离是(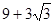 )km.试画出大致示意图,并计算出从A到D的方位角和距离(结果保留根号).
)km.试画出大致示意图,并计算出从A到D的方位角和距离(结果保留根号). 中,
中,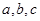 分别是角
分别是角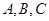 的对边,且
的对边,且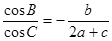 .
.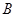 的大小;
的大小;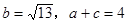 ,求
,求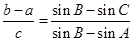 ,关于x的不等式x2cosC+4xsinC+6≥0对任意的x∈R恒成立.
,关于x的不等式x2cosC+4xsinC+6≥0对任意的x∈R恒成立. .
. 的最小正周期和值域;
的最小正周期和值域; 中,角
中,角 的对边分别为
的对边分别为 ,若
,若 且
且 ,
,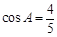 ,求
,求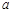 和
和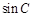 .
. 中,角
中,角 所对的边分别为
所对的边分别为 ,已知
,已知 ,
, ,
, ,求
,求 .
. 中,角A、B、C的对边分别为a、b、c,S是该三角形的面积
中,角A、B、C的对边分别为a、b、c,S是该三角形的面积 ,
, 求角B的度数
求角B的度数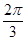 ,S=
,S= ,求b的值
,求b的值 .
. -cos 2A的值.
-cos 2A的值. ,求bc的最大值.
,求bc的最大值.