题目内容
已知x>0,y>0,且x+y=4,则使不等式
+
≥m恒成立的实数m的取值范围是( )
| 1 |
| x |
| 4 |
| y |
A、(-∞,
| ||
B、[
| ||
C、(-∞,
| ||
D、[
|
考点:基本不等式
专题:不等式的解法及应用
分析:利用“乘1法”与基本不等式的性质即可得出.
解答:
解:∵x>0,y>0,且x+y=4,
则使不等式
+
=
(x+y)(
+
)=
(5+
+
)≥
(5+2
)=
≥m(当且仅当y=2x=
取等号)恒成立的实数m的取值范围是:m≤
.
故选:A.
则使不等式
| 1 |
| x |
| 4 |
| y |
| 1 |
| 4 |
| 1 |
| x |
| 4 |
| y |
| 1 |
| 4 |
| y |
| x |
| 4x |
| y |
| 1 |
| 4 |
|
| 9 |
| 4 |
| 8 |
| 3 |
| 9 |
| 4 |
故选:A.
点评:本题考查了“乘1法”与基本不等式的性质,属于基础题.

练习册系列答案
 开心蛙口算题卡系列答案
开心蛙口算题卡系列答案
相关题目
若y=Asin(ωx+φ)(A>0,ω>0,|φ|<
)的最小值巍峨-2,其图象相邻最高点与最低点横坐标之差为2π,且图象过点(0,1),则其解析式是( )
| π |
| 2 |
A、y=2sin(
| ||||
B、y=2sin(
| ||||
C、y=2sin(x+
| ||||
D、y=2sin(x+
|
直线(2m2-5m-3)x-(m2-9)y+4=0的倾斜角为
,则m的值是( )
| π |
| 4 |
| A、3 | B、2 | C、-2 | D、2与3 |
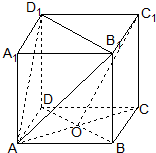 已知正方体ABCD-A1B1C1D1,O是底面ABCD对角线的交点.
已知正方体ABCD-A1B1C1D1,O是底面ABCD对角线的交点.