题目内容
8.设函数f(x)=x2-2ax+15-2a的两个零点分别为x1,x2,且在区间(x1,x2)上恰好有两个正整数,则实数a的取值范围($\frac{31}{10}$,$\frac{19}{6}$].分析 由题意可得函数y=$\frac{{x}^{2}+15}{x+1}$的图象和直线y=2a有两个交点,这2个交点的横坐标分别为x1,x2,在区间(x1,x2)上恰有两个正整数.再令x+1=t,则m(t)=t+$\frac{16}{t}$的图象和直线y=2a+2有两个交点,这2个交点的横坐标分别为t1,t2,则在区间(t1,t2)上恰有两个正整数,求得a的范围.
解答 解:令f(x)=0,可得x2 +15=2a(x+1),
即$\frac{{x}^{2}+15}{x+1}$=2a,
由题意可得方程$\frac{{x}^{2}+15}{x+1}$=2a 有2个解x1,x2,
且在区间(x1,x2)上恰有两个正整数,
故函数y=$\frac{{x}^{2}+15}{x+1}$的图象和直线y=2a有两个交点,
且这2个交点的横坐标分别为x1,x2.
再令x+1=t,则y=$\frac{{(t-1)}^{2}+15}{t}$=t+$\frac{16}{t}$-2,
即m(t)=t+$\frac{16}{t}$的图象和直线y=2a+2有两个交点,
且这2个交点的横坐标分别为t1,t2,
在区间(t1,t2)上恰有两个正整数,而这两个正整数应为4和5.
令t=5,则m(t)=$\frac{41}{5}$,令t=3,则m(t)=$\frac{25}{3}$,
∴$\frac{41}{5}$<2a+2≤$\frac{25}{3}$,求得$\frac{31}{10}$<a≤$\frac{19}{6}$,
故符合条件的a的范围是:{a|$\frac{31}{10}$<a≤$\frac{19}{6}$}.
故答案为:($\frac{31}{10}$,$\frac{19}{6}$].
点评 本题主要考查一元二次方程根的分布与系数的关系,函数的图象,函数零点的定义,属于中档题.

| A. | -3-2i | B. | -3+2i | C. | 2+3i | D. | 3-2i |
| A. | 1+i | B. | 1-i | C. | 2i | D. | -2i |
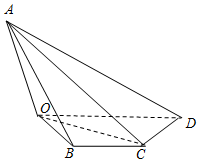 如图,四棱锥A-OBCD中,已知平面AOC⊥面OBCD,AO=2$\sqrt{3}$,OB=BC=2,CD=4,∠OBC=∠BCD=120°.
如图,四棱锥A-OBCD中,已知平面AOC⊥面OBCD,AO=2$\sqrt{3}$,OB=BC=2,CD=4,∠OBC=∠BCD=120°.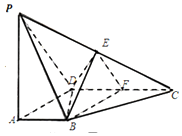 如图,在四棱锥P-ABCD中,PA⊥平面ABCD,∠DAB为直角,AB∥CD,AD=CD=2AB=2,E,F分别为PC,CD的中点.
如图,在四棱锥P-ABCD中,PA⊥平面ABCD,∠DAB为直角,AB∥CD,AD=CD=2AB=2,E,F分别为PC,CD的中点.