题目内容

设△ABC中，tanA+tanB+
3
=
3
tanAtanB，cosAcosB=1-sinAsinB，则此三角形是______三角形．
∵tanA+tanB+
3
=
3
tanAtanB?tanA+tanB=
3
tanAtanB-
3
?tan（A+B）=
tanA+tanB
1-tanAtanB
=-
3
．
∴A+B=120°；
∵cosAcosB=1-sinAsinB?cosAcosB+sinAsinB=1?cos（A-B）=1?A=B
∴A=B=60°．
故答案为：等边
练习册系列答案
相关题目
已知△ABC中，2sinAcosB=sinCcosB+cosCsinB．
（Ⅰ）求角B的大小；
（Ⅱ）设向量
m
=（cosA，cos2A），
n
=(-
12
5
， 1)，求当
m
•
n
取最小值时，tan(A-
π
4
)值．
在△ABC中，设内角A、B、C的对边分别为a、b、c，且tan(
π
4
-C)=
3
-2
（1）求角C的大小；
（2）若c=
7
且a+b=5求△ABC的面积．
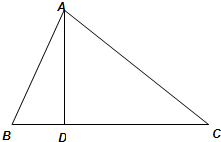如图，在△ABC中，AD为BC边上的高，垂足D在边BC上，∠CAD=2∠BAD=2θ（0＜θ＜
π
4
），BD=1，设△ABD，△ACD的面积分别为S1，S2．
（Ⅰ）当
S2
S1
＞4时，求tanθ的取值范围；
（Ⅱ）当S1S2＞
9
4
时，求tanθ的取值范围．
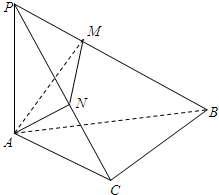如图所示，在斜边为AB的Rt△ABC中，过A作PA⊥平面ABC，AM⊥PB于M，
AN⊥PC于N．（Ⅰ）求证：BC⊥面PAC；
（Ⅱ）求证：PB⊥面AMN．
（Ⅲ）若PA=AB=4，设∠BPC=θ，试用tanθ表示△AMN 的面积，当tanθ取何值时，△AMN的面积最大？最大面积是多少？
在△ABC中，已知角A、B、C所对的边分别是a、b、c，且a=2，∠A=
π
4
，设∠C=θ．
（1）θ表示b；
（2）若tanθ=-
4
3
，求
CA
•
CB
的值．

违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com

精英家教网