题目内容
三棱柱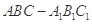 中,侧棱
中,侧棱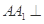 底面
底面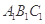 ,底面三角形
,底面三角形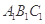 是正三角形,
是正三角形,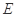 是
是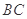 中点,则下列叙述正确的是( )
中点,则下列叙述正确的是( )
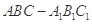 中,侧棱
中,侧棱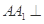 底面
底面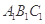 ,底面三角形
,底面三角形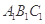 是正三角形,
是正三角形,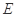 是
是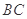 中点,则下列叙述正确的是( )
中点,则下列叙述正确的是( )A.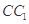 与 与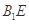 是异面直线 是异面直线 |
B.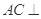 平面 平面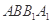 |
C.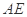 、 、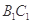 为异面直线,且 为异面直线,且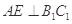 |
D.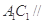 平面 平面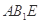 |
C
试题分析:作出草图:知
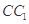 与
与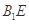 都在平面BCC1B1内,所以不是异面直线;对于B,取AB的中点为F,联结CF,由于底面三角形
都在平面BCC1B1内,所以不是异面直线;对于B,取AB的中点为F,联结CF,由于底面三角形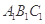 是正三角形,所以CF
是正三角形,所以CF AB,又因为侧棱
AB,又因为侧棱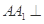 底面
底面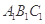 ,所以
,所以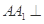 底面ABC,从而有CF
底面ABC,从而有CF AA1,所以有CF
AA1,所以有CF 平面
平面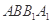 ,而过一点有且只有一条直线和一个平面垂直,故AC与平面
,而过一点有且只有一条直线和一个平面垂直,故AC与平面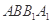 不可能垂直;同理可知AE
不可能垂直;同理可知AE 平面BCC1B1,所以
平面BCC1B1,所以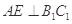 ,显然
,显然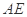 、
、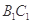 为异面直线,故选C.
为异面直线,故选C.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
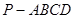 的底面为菱形,
的底面为菱形,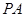
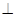 面
面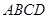 ,且
,且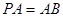 ,
,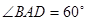 ,
,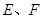 分别是
分别是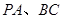 的中点.
的中点.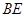 ∥平面
∥平面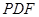 ;
;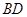 作一平面交棱
作一平面交棱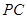 于点
于点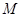 ,若二面角
,若二面角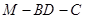 的大小为
的大小为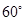 ,求
,求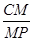 的值.
的值.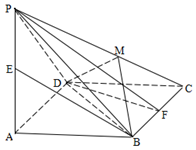
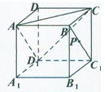
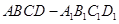 中,
中,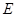 是
是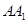 的中点.
的中点.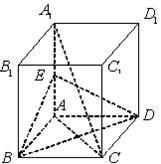
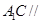 平面
平面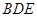 ;
;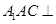 平面
平面 所成角的正弦值.
所成角的正弦值.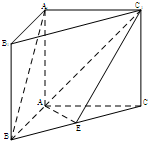
 ,
,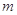 ,
,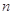 为三条不同的直线,
为三条不同的直线,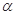 ,
,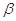 为两个不同的平面,下列命题中正确的是( )
为两个不同的平面,下列命题中正确的是( ) 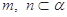 ,则
,则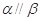 .
.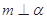 ,
,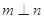 ,则
,则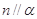 .
.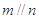 ,
,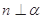 ,则
,则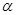 、
、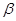 和直线
和直线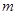 ,给出条件:①
,给出条件:①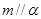 ;②
;②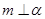 ;③
;③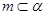 ;④
;④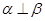 ;⑤
;⑤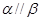 .
.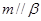 的是( )
的是( )