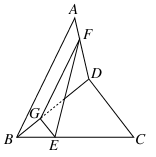
题目内容
如图,在正方体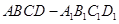 中,
中,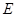 是
是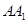 的中点.
的中点.
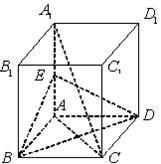
(1)求证: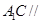 平面
平面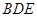 ;
;
(2)求证:平面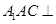 平面
平面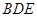 ;
;
(3)求直线BE与平面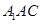 所成角的正弦值.
所成角的正弦值.
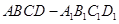 中,
中,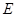 是
是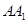 的中点.
的中点.
(1)求证:
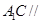 平面
平面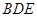 ;
;(2)求证:平面
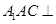 平面
平面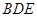 ;
;(3)求直线BE与平面
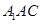 所成角的正弦值.
所成角的正弦值.(1)见解析;(2)见解析;(3) 。
。
 。
。试题分析:(1)设
 ,证明
,证明 即可;(2)证明
即可;(2)证明 ,
, ,则
,则 ;(3)根据线面角的定义结合(2)可知直线BE与平面
;(3)根据线面角的定义结合(2)可知直线BE与平面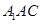 所成角是∠BEO。
所成角是∠BEO。 (1)设
 ,
,
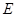 、
、 分别是
分别是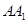 、
、 的中点,
的中点,
 ∥
∥
又
 平面
平面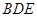 ,
, 平面
平面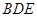 ,
,
 ∥平面
∥平面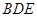 4分
4分(2)

 平面
平面 ,
, 平面
平面 ,
, 5分
5分又
 ,
, ,
,
 平面
平面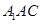 7分
7分 平面
平面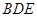 ,
, 平面
平面 平面
平面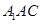 8分
8分(3)由(2)可知直线BE与平面
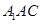 所成角是∠BEO 9分
所成角是∠BEO 9分设正方体棱长为a,在Rt△BOE中,
 11分
11分∴
 ,即直线BE与平面
,即直线BE与平面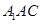 所成角的正弦值为
所成角的正弦值为 12分
12分
练习册系列答案
相关题目

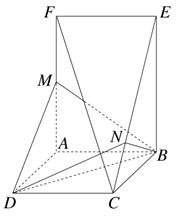
 中, 四边形
中, 四边形 是正方形,
是正方形, ,
, .将正方形沿
.将正方形沿 折起,得到如图2所示的多面体,其中面
折起,得到如图2所示的多面体,其中面 面
面 ,
, 是
是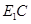 中点.
中点. ∥平面
∥平面 ;
; 的体积.
的体积.

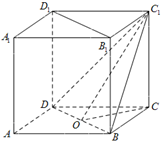
 且
且 ,给出下列命题:
,给出下列命题: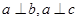 则
则 ②
②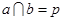 则
则
 ④若
④若 则
则
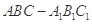 中,侧棱
中,侧棱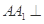 底面
底面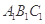 ,底面三角形
,底面三角形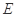 是
是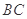 中点,则下列叙述正确的是( )
中点,则下列叙述正确的是( )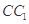 与
与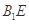 是异面直线
是异面直线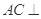 平面
平面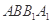
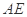 、
、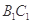 为异面直线,且
为异面直线,且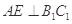
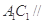 平面
平面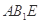
 ,求AB和CD所成角的余弦值.
,求AB和CD所成角的余弦值.