题目内容
已知平面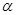 、
、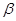 和直线
和直线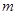 ,给出条件:①
,给出条件:①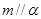 ;②
;②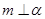 ;③
;③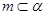 ;④
;④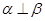 ;⑤
;⑤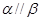 .
.
由这五个条件中的两个同时成立能推导出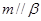 的是( )
的是( )
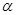 、
、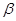 和直线
和直线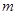 ,给出条件:①
,给出条件:①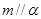 ;②
;②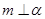 ;③
;③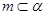 ;④
;④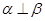 ;⑤
;⑤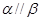 .
.由这五个条件中的两个同时成立能推导出
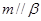 的是( )
的是( )| A.①④ | B.①⑤ | C.②⑤ | D.③⑤ |
D
试题分析:对于A选项,若
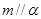 且
且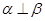 ,则
,则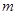 与
与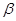 的位置关系不确定,A选项错误;对于B选项,若
的位置关系不确定,A选项错误;对于B选项,若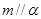 且
且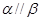 ,则
,则 或
或 ,B选项也不正确;对于C选项,若
,B选项也不正确;对于C选项,若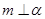 且
且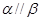 ,则
,则 ,C选项也错误;对于D选项,若
,C选项也错误;对于D选项,若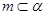 且
且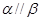 ,则直线
,则直线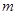 与平面
与平面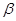 无公共点,故D选项正确,故选D.
无公共点,故D选项正确,故选D.
练习册系列答案
 海淀课时新作业金榜卷系列答案
海淀课时新作业金榜卷系列答案 期末金牌卷系列答案
期末金牌卷系列答案 轻松课堂标准练系列答案
轻松课堂标准练系列答案
相关题目
 中,底面
中,底面 为矩形,
为矩形, 平面
平面 是
是 的中点.
的中点. //平面
//平面 ;
; ,三棱锥
,三棱锥 的体积
的体积 ,求
,求 到平面
到平面 的距离.
的距离.
 ,DC⊥平面ABC,EB⊥平面ABC, AB=AC=BE=2,CD=1.
,DC⊥平面ABC,EB⊥平面ABC, AB=AC=BE=2,CD=1. ,求证:
,求证:
 的中点,O1,O1′,O2,O2′分别为CD,C′D′,DE,D′E′的中点.
的中点,O1,O1′,O2,O2′分别为CD,C′D′,DE,D′E′的中点.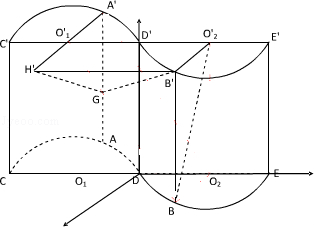
 中, 四边形
中, 四边形 是正方形,
是正方形, ,
, .将正方形沿
.将正方形沿 折起,得到如图2所示的多面体,其中面
折起,得到如图2所示的多面体,其中面 面
面 ,
, 是
是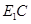 中点.
中点. ∥平面
∥平面 ;
; 的体积.
的体积.

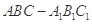 中,侧棱
中,侧棱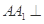 底面
底面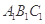 ,底面三角形
,底面三角形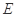 是
是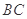 中点,则下列叙述正确的是( )
中点,则下列叙述正确的是( )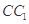 与
与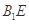 是异面直线
是异面直线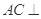 平面
平面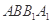
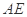 、
、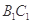 为异面直线,且
为异面直线,且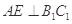
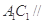 平面
平面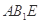
 ,求AB和CD所成角的余弦值.
,求AB和CD所成角的余弦值.
 ACB=
ACB= ,PA
,PA 平面ABC,
平面ABC,