题目内容
已知复数z1=i(1-i)3,(1)求|z1|;
(2)若|z|=1,求|z-z1|的最大值.
思路解析:(1)求模应求出复数的实部与虚部再利用|a+bi|=![]() 得出;
得出;
(2)是考查复数几何意义的应用.
解:(1)z1=i(1-i)3=i(-2i)(1-i)=2(1-i),∴|z1|=![]() .
.
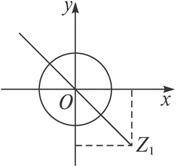
(2)|z|=1可看成半径为1圆心为(0,0)的圆,而z1可看成在坐标系中的点(2,-2),
∴|z-z1|的最大值可以看成点(2,-2)到圆上点距离的最大值,
由图可知|z-z1|max=![]() +1.
+1.
变式方法:|z|=1,∴设z=cosθ+isinθ,
|z-z1|=|cosθ+isinθ-2+2i|=![]() .
.
当sin(θ-![]() )=-1时,|z-z1|2取得最大值
)=-1时,|z-z1|2取得最大值![]() .
.
从而得到|z-z1|的最大值为![]() .
.
方法归纳 注意此处空半格在设复数的过程中常设为z=a+bi(a、b∈R);在有关的解决轨迹问题中常设z=x+yi从而与解析几何联系起来;当复数的模为1时也可以设为z=cosθ+isinθ用三角函数解决相关最值等.

练习册系列答案
 七星图书口算速算天天练系列答案
七星图书口算速算天天练系列答案
相关题目