题目内容
过点P(1,2)的直线l被两平行线l1:4x+3y+1=0与l2:4x+3y+6=0截得的线段长|AB|=
,求直线l的方程.
| 2 |
分析:根据题意,先验证直线l的斜率不存在时,不满足|AB|=
.然后设直线l的方程为y-2=k(x-1),分别求出A、B含有字母k的坐标,用两点的距离公式列出关于k的方程,解之即可得到直线的斜率k值,从而得到直线l的方程.
| 2 |
解答:解:当直线l的斜率不存在时,方程为x=1,经验证|AB|=
,不符合题意
故可设直线l的方程为y-2=k(x-1),与l1:4x+3y+1=0联解,得A(
,
)
同理,可得直线l与l2:4x+3y+6=0交于点B(
,
)
∵|AB|=
,
∴
=
,
整理得7k2-48k-7=0,解之得k=7或-
∴直线l的方程为y-2=7(x-1)或y-2=-
(x-1),
化简整理得,所求直线l的方程为7x-y-5=0或x+7y-15=0.
| 5 |
| 3 |
故可设直线l的方程为y-2=k(x-1),与l1:4x+3y+1=0联解,得A(
| 3k-7 |
| 3k+4 |
| -5k+8 |
| 3k+4 |
同理,可得直线l与l2:4x+3y+6=0交于点B(
| 3k-12 |
| 3k+4 |
| 8-10k |
| 3k+4 |
∵|AB|=
| 2 |
∴
(
|
| 2 |
整理得7k2-48k-7=0,解之得k=7或-
| 1 |
| 7 |
∴直线l的方程为y-2=7(x-1)或y-2=-
| 1 |
| 7 |
化简整理得,所求直线l的方程为7x-y-5=0或x+7y-15=0.
点评:本题给出动直线被平行直线截得的弦长,求直线的方程,着重考查了直线方程的基本形式、直线与直线的位置关系等知识,属于基础题.

练习册系列答案
 学而优衔接教材南京大学出版社系列答案
学而优衔接教材南京大学出版社系列答案 小学课堂作业系列答案
小学课堂作业系列答案 金博士一点全通系列答案
金博士一点全通系列答案
相关题目

 椭圆E:
椭圆E: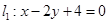 与
与 的交点为P,直
的交点为P,直 的方程为:
的方程为: .
. 过点A(a,0),B(0,b)的直
过点A(a,0),B(0,b)的直 ,原点到该直线的距离为
,原点到该直线的距离为 .
. 求直线MN的方程;
求直线MN的方程; 交椭圆于P、Q两点,以PQ为直径的圆过点D(1,0)?若存在,求出k的值;若不存在,请说明理由。
交椭圆于P、Q两点,以PQ为直径的圆过点D(1,0)?若存在,求出k的值;若不存在,请说明理由。