题目内容
15.定义在实数集R上的函数f(x)是周期为2的周期函数,且当x∈[-1,1]时,$f(x)=\left\{\begin{array}{l}{2^x}+1(0≤x≤1)\\{2^{-x}}+1(-1≤x<0)\end{array}\right.$.请设计计算f(x)的函数值的算法程序框图.分析 根据题目已知中分段函数的解析式$f(x)=\left\{\begin{array}{l}{2^x}+1(0≤x≤1)\\{2^{-x}}+1(-1≤x<0)\end{array}\right.$.然后根据分类标准,设置两个判断框的并设置出判断框中的条件,再由函数各段的解析式,确定判断框的“是”与“否”分支对应的操作,由此即可画出流程图,再编写满足题意的程序
解答 解:(1)将$f(x)=\left\{\begin{array}{l}{2^x}+1(0≤x≤1)\\{2^{-x}}+1(-1≤x<0)\end{array}\right.$
变形为:f(x)=2|x|+1,-1≤x≤1
(2)按原函数设计的程序框图如图②
设计的程序框图如图①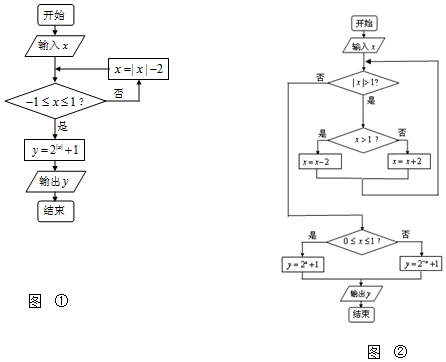
点评 本题考查了设计程序框图解决实际问题.主要考查编写程序解决分段函数问题.

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目
3.某人抛掷一枚质地均匀的硬币100次,结果出现了50次正面向上.如果他将这枚硬币抛掷1000次,那么出现正面向上的次数,在下面四个选项中,最合适的选项是( )
| A. | 恰为500次 | B. | 恰为600次 | C. | 500次左右 | D. | 600次左右 |
20.为了解适龄公务员对开放生育二胎政策的态度,某部门随机调查了90位三十岁到四十岁的公务员,得到如下列联表,因不慎丢失部分数据.
(1))完成表格数据,判断是否有99%以上的把握认为“生二胎意愿与性别有关”并说明理由;
(2)现从有意愿生二胎的45人中随机抽取2人,求男性公务员和女性公务员各一人的概率.
附:k2=$\frac{{n{{(ad-bc)}^2}}}{(a+b)(c+d)(a+c)(b+d)}$.
(1))完成表格数据,判断是否有99%以上的把握认为“生二胎意愿与性别有关”并说明理由;
(2)现从有意愿生二胎的45人中随机抽取2人,求男性公务员和女性公务员各一人的概率.
| 男性公务员 | 女性公务员 | 总计 | |
| 有意愿生二胎 | 30 | 15 | 45 |
| 无意愿生二胎 | 20 | 25 | 45 |
| 总计 | 50 | 40 | 90 |
| P(k2≥k0) | 0.050 | 0.010 | 0.001 |
| k0 | 3.841 | 6.635 | 10.828 |
7.命题p:关于x的方程x2+ax+2=0无实根,命题q:函数f(x)=logax在(0,+∞)上单调递增,若“p∧q”为假命题,“p∨q”真命题,则实数a的取值范围是( )
| A. | (-2$\sqrt{2}$,+∞) | B. | (-2$\sqrt{2}$,2$\sqrt{2}$) | C. | (-2$\sqrt{2}$,1]∪[2$\sqrt{2}$,+∞) | D. | (-∞,2$\sqrt{2}$) |
4.设抛物线x2=2py (P>0),M为直线y=-2p上任意一点,过M引抛物线的切线,切点分别为A,B,A,B,M的横坐标分别为XA,XB,XM则( )
| A. | XA+XB=2XM | B. | XA•XB=X${\;}_{M}^{2}$ | C. | $\frac{1}{{X}_{A}}$+$\frac{1}{{X}_{B}}$=$\frac{2}{{X}_{M}}$ | D. | 以上都不对 |
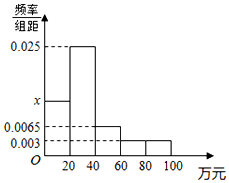 某市随机抽取部分企业调查年上缴税收情况(单位:万元),将所得数据绘制成频率分布直方图(如图),年上缴税收范围是[0,100],样本数据分组为第一组[0,20),第二组AA1⊥平面ABC,第三组[40,60),第四组[60,80),第五组[80,100].
某市随机抽取部分企业调查年上缴税收情况(单位:万元),将所得数据绘制成频率分布直方图(如图),年上缴税收范围是[0,100],样本数据分组为第一组[0,20),第二组AA1⊥平面ABC,第三组[40,60),第四组[60,80),第五组[80,100]. 如图是某赛季甲、乙两名篮球运动员每场比赛得分情况的茎叶图.从这个茎叶图可以看出甲、乙两名运动员得分的中位数分别是35,26.
如图是某赛季甲、乙两名篮球运动员每场比赛得分情况的茎叶图.从这个茎叶图可以看出甲、乙两名运动员得分的中位数分别是35,26.