题目内容
定义在区间[-
π,π]上的函数y=f(x)的图象关于直线x=
对称,当x∈[-
π,
]时,函数f(x)=Asin(ωx+φ)(A>0,ω>0,0<φ<π),其图象如图所示.

(Ⅰ)求函数y=f(x)在[-
π,π]的表达式;
(Ⅱ)求方程f(x)=
的解;
(Ⅲ)是否存在常数m的值,使得|f(x)-m|<2在x∈[-
,π]上恒成立;若存在,求出m的取值范围;若不存在,请说明理由.
| 2 |
| 3 |
| π |
| 6 |
| 2 |
| 3 |
| π |
| 6 |

(Ⅰ)求函数y=f(x)在[-
| 2 |
| 3 |
(Ⅱ)求方程f(x)=
| 2 |
(Ⅲ)是否存在常数m的值,使得|f(x)-m|<2在x∈[-
| 2π |
| 3 |
(Ⅰ)x∈[-
,
],A=2,
=-
-(-
),∴T=2π,ω=1,
且f(x)=2sin(x+φ)过(-
,2),
∵0<φ<π,∴-
+φ=
,φ=
,
f(x)=2sin(x+
),
当
≤x≤π时,-
≤
-x≤
,f(
-x)=2sin(
-x+
)=2sin(π-x)=2sinx,
而函数y=f(x)的图象关于直线x=
对称,则f(x)=f(
-x),即f(x)=2sinx,
≤x≤π,
∴f(x)=
;
(Ⅱ)当-
≤x≤
时,f(x)=2sin(x+
)=
,sin(x+
)=
,
∴x+
=
或
,即x=-
或
,
当
≤x≤π时,f(x)=2sinx=
,sinx=
,∴x=
或
,
∴方程f(x)=
的解集是{-
,
,
,
},
(Ⅲ)存在,假设存在,由条件得:m-2<f(x)<m+2在x∈[-
,π]上恒成立,
即
,
由图象可得:
,解得0<m<2.
| 2π |
| 3 |
| π |
| 6 |
| T |
| 4 |
| π |
| 6 |
| 2π |
| 3 |
且f(x)=2sin(x+φ)过(-
| π |
| 6 |
∵0<φ<π,∴-
| π |
| 6 |
| π |
| 2 |
| 2π |
| 3 |
f(x)=2sin(x+
| 2π |
| 3 |
当
| π |
| 6 |
| 2π |
| 3 |
| π |
| 3 |
| π |
| 6 |
| π |
| 3 |
| π |
| 3 |
| 2π |
| 3 |
而函数y=f(x)的图象关于直线x=
| π |
| 6 |
| π |
| 3 |
| π |
| 6 |
∴f(x)=
|
(Ⅱ)当-
| 2π |
| 3 |
| π |
| 6 |
| 2π |
| 3 |
| 2 |
| 2π |
| 3 |
| ||
| 2 |
∴x+
| 2π |
| 3 |
| π |
| 4 |
| 3π |
| 4 |
| 5π |
| 12 |
| π |
| 12 |
当
| π |
| 6 |
| 2 |
| ||
| 2 |
| π |
| 4 |
| 3π |
| 4 |
∴方程f(x)=
| 2 |
| 5π |
| 12 |
| π |
| 12 |
| π |
| 4 |
| 3π |
| 4 |
(Ⅲ)存在,假设存在,由条件得:m-2<f(x)<m+2在x∈[-
| 2π |
| 3 |
即
|
由图象可得:
|

练习册系列答案
相关题目
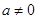 ,函数
,函数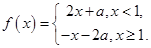 若
若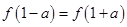 ,则
,则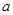 的值为________.
的值为________. 若f(a)+f(-1)=2,则a等于( ).
若f(a)+f(-1)=2,则a等于( ).