题目内容

19．若sinα＜0，tanα＞0，则α的终边在（　　）
A．第一象限B．、第二象限C．第三象限D．第四象限

分析 根据题意和“一全正、二正弦、三正切、四余弦”进行判断α终边所在的位置．

解答 解：sinα＜0，则α的终边在三、四象限或y轴的负半轴上； tanα＞0则α的终边在三、一象限，
sinα＜0，tanα＞0，同时满足，则α的终边在三象限．
故选：C

点评 本题考查了三角函数值的符号判断，需要利用题中三角函数的不等式和“一全正、二正弦、三正切、四余弦”对角的终边位置进行判断，是基础题．

练习册系列答案
相关题目
9．已知P1（2，-1），P2（0，5），点P在线段P1P2的延长线上，且|$\overrightarrow{{P}_{1}P}$|=2|$\overrightarrow{P{P}_{2}}$|，则点P的坐标（　　）
A．（4，-7）B．（-2，11）C．（4，-7）和（-2，11）D．（-2，11）和（1，2）
10．等比数列{an}各项均为正数，且a5a6+a4a7=54，则log3a1+log3a2+…+log3a10=（　　）
A．8B．10C．15D．20
7．设F1，F2为椭圆C：$\frac{{x}^{2}}{{a}^{2}}$+$\frac{{y}^{2}}{{b}^{2}}$=1（a＞b＞0）的焦点，过F2在的直线交椭圆于A，B两点，AF1⊥AB且AF1=AB，则椭圆C的离心率为$\sqrt{6}$-$\sqrt{2}$．
14．200辆汽车通过某一段公路时的时速的频率分布直方图如图所示，则时速在[50，70）的汽车大约（　　）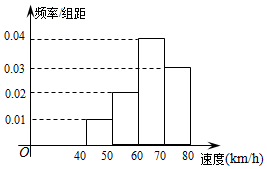
A．60辆B．80辆C．100辆D．120辆
4．有一段“三段论”，其推理是这样的：
对于可导函数f（x），若f′（x0）=0，则x=x0是函数f（x）的极值点…大前提因为函数f（x）=x3满足f′（0）=0，…小前提所以x=0是函数f（x）=x3的极值点”，结论以上推理（　　）
A．大前提错误B．小前提错误C．推理形式错误D．没有错误
11．已知$\overrightarrow a$，$\overrightarrow b$满足：$|\overrightarrow a|=3$，$|\overrightarrow b|=2$，$\overrightarrow a•\overrightarrow b=\frac{3}{2}$，则$|\overrightarrow a-\overrightarrow b|$=（　　）
A．$\sqrt{10}$B．$\sqrt{5}$C．3D．10
8．如果a＜b＜0，那么下列不等式成立的是（　　）
A．$\frac{1}{a}＜\frac{1}{b}$B．a+c＜b+cC．a-c＞b-cD．a•c＜b•c
9．已知全集U={-1，2，3，a}，集合M={-1，3}．若∁UM={2，5}，则实数a的值为5．

违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com

精英家教网