Question

如下图，M是抛物线y²=x上的一个定点，弦ME、MF分别交x轴于A、B两点，且MA=MB.证明直线EF的斜率为定值.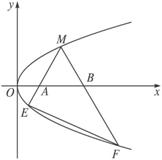

Answer 1

思路点拨：本题要证明直线EF的斜率为定值，不难想到这个定值与定点M有关，因此在解决过程中，不难想到先假设定点M的坐标，从而结合已知条件将其斜率表示出来得到结果.

解：设M(y₀²,y₀)，直线ME的斜率为k(k＞0)，则直线MF的斜率为-k，方程为y-y₀=k(x-y₀²).

由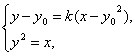消x得ky²-y+y₀(1-ky₀)=0，解得y_E=

∴x_E=,同理可求得y_F=,x_F=,

 

∴k_EF=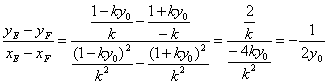(定值)，所以直线EF的斜率为定值.

［一通百通］ 对于有关抛物线与直线的交点问题，处理的方法通常是联立直线方程与抛物线方程消去其中一个未知数，但对于具体问题来说，通常要因问题而定，如果相应的交点坐标不难解出，这时可以考虑具体找到交点坐标从而将问题解决.