题目内容
求函数y=f(x)=(
) x-(
) x+1,x∈［-3,2］的值域.
解析：将()x看作一个未知量t,把原函数转化为关于t的二次函数求解.
答案：
∵f(x)=［()x］2-(
) x+1,x∈［-3,2］,?
∴(
)2≤(
)x≤(
)-3,即
≤(
)x≤8.
设t=(
) x,则
≤t≤8.?
将函数化为f(t)=t 2-t+1,t∈［
,8］.?
∵f(t)=(t-
) 2+
,
∴f(
)≤f(t)≤f(8).?
∴
≤f(t)≤57.
∴函数的值域为［
,57］.
练习册系列答案
相关题目
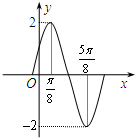（2012•咸阳三模）已知函数f（x）=Asin（ωx+φ）（其中