题目内容
（2012•咸阳三模）已知函数f（x）=Asin（ωx+φ）（其中A＞0，ω＞0，0＜φ＜| π |
| 2 |
（1）求函数y=f（x）的解析式；
（2）求函数y=f(x+
| π |
| 8 |
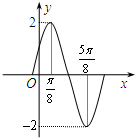
分析：（1）由图知A=2，T=2(
-
)=π，可求ω的值，利用最高点的坐标，可求φ的值，从而可得函数的解析式；
（2）令函数y=f(x+
)=0，解方程，可得函数y=f(x+
)的零点．
| 5π |
| 8 |
| π |
| 8 |
（2）令函数y=f(x+
| π |
| 8 |
| π |
| 8 |
解答：解：（1）由图知A=2，T=2(
-
)=π，∴ω=2…（3分）
∴f（x）=2sin（2x+φ）
又∵f(
)=2sin(
+φ)=2
∴sin（
+φ）=1，
∴
+φ=
+2kπ，∴φ=
+2kπ，（k∈Z）
∵0＜φ＜
，∴φ=
∴函数的解析式为f(x)=2sin(2x+
)…（6分）
（2）由（1）知：f(x)=2sin(2x+
)，
∴f(x+
)=2sin(2x+
)=2cos2x=0…（9分）
∴2x=kπ+
，即x=
+
(k∈Z)
∴函数y=f(x+
)的零点为x=
+
(k∈Z)…（12分）
| 5π |
| 8 |
| π |
| 8 |
∴f（x）=2sin（2x+φ）
又∵f(
| π |
| 8 |
| π |
| 4 |
∴sin（
| π |
| 4 |
∴
| π |
| 4 |
| π |
| 2 |
| π |
| 4 |
∵0＜φ＜
| π |
| 2 |
| π |
| 4 |
∴函数的解析式为f(x)=2sin(2x+
| π |
| 4 |
（2）由（1）知：f(x)=2sin(2x+
| π |
| 4 |
∴f(x+
| π |
| 8 |
| π |
| 2 |
∴2x=kπ+
| π |
| 2 |
| kπ |
| 2 |
| π |
| 4 |
∴函数y=f(x+
| π |
| 8 |
| kπ |
| 2 |
| π |
| 4 |
点评：本题考查三角函数解析式的求解，考查函数的零点，考查学生的读图能力，属于中档题．
练习册系列答案
相关题目
（2012•咸阳三模）从一个棱长为1的正方体中切去一部分，得到一个几何体，其三视图如图，则该几何体的体积为（ ）