题目内容
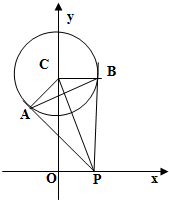 已知圆C:x2+(y-2)2=1,过P(1,0),作圆C的切线,切点A,B.
已知圆C:x2+(y-2)2=1,过P(1,0),作圆C的切线,切点A,B.(1)求直线PA、PB的直线方程;
(2)求弦长|AB|;
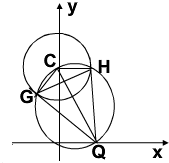
(3)若Q点是x轴上的动点,过Q点作圆C的切线.切点为G、H,求四边形GCHQ的面积的最小值.
考点:直线与圆锥曲线的综合问题
专题:圆锥曲线中的最值与范围问题
分析:(1)若k存在,设直线PA:y=k(x-1),由圆心到切线距离等于半径,能求出直线PA;若k不存在,PB:x=1也是圆的一条切线.
(2)利用等面积法能求出|AB|.
(3)设Q(m,0),S四边形GCHQ=GH×QH,由此能求出当Q(0,0)时,四边形GCHQ的面积的最小值为
.
(2)利用等面积法能求出|AB|.
(3)设Q(m,0),S四边形GCHQ=GH×QH,由此能求出当Q(0,0)时,四边形GCHQ的面积的最小值为
| 3 |
解答:
解:(1)圆C:x2+(y-2)2=1,过P(1,0),
作圆C的切线,切点A,B,
若k存在,设直线PA:y=k(x-1),
d=
=1,解得k=-
,
∴直线PA:y=-
(x-1),整理,得3x+4y-3=0.
若k不存在,PB:x=1也是圆的一条切线,
∴直线PB:x=1.
(2)∵半径r=1,PC=
,PB=2,
∴
PC×
=
BC×BP,
∴AB=
×2=
.
(3)设Q(m,0),
S四边形GCHQ=GH×QH,
∵CQ=
,QH=
=
,
∴S四边形GCHQ=
≥
,
∴当Q(0,0)时,四边形GCHQ的面积的最小值为
.
作圆C的切线,切点A,B,
若k存在,设直线PA:y=k(x-1),
d=
| |2+k| | ||
|
| 3 |
| 4 |

∴直线PA:y=-
| 3 |
| 4 |
若k不存在,PB:x=1也是圆的一条切线,
∴直线PB:x=1.
(2)∵半径r=1,PC=
| 5 |
∴
| 1 |
| 2 |
| AB |
| 2 |
| 1 |
| 2 |
∴AB=
| BC×BP |
| PC |
4
| ||
| 5 |
(3)设Q(m,0),
S四边形GCHQ=GH×QH,
∵CQ=
| m2+4 |
| CQ2-CH2 |
| m2+3 |
∴S四边形GCHQ=
| m2+3 |
| 3 |
∴当Q(0,0)时,四边形GCHQ的面积的最小值为
| 3 |
点评:本题考查圆的切线方程的求法,考查弦长的求法,考查四边形面积的最小值的求法,解题时要认真审题,注意点到直线的距离公式的合理运用.

练习册系列答案
相关题目
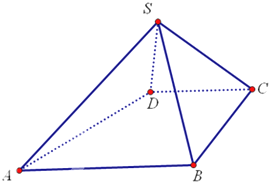 如图,四棱锥S-ABCD中,AB∥CD,BC⊥CD,侧面SAB为等边三角形.AB=BC=2,CD=SD=1.
如图,四棱锥S-ABCD中,AB∥CD,BC⊥CD,侧面SAB为等边三角形.AB=BC=2,CD=SD=1.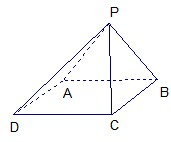 已知四棱锥P-ABCD的底面为菱形,且∠ABC=60°,AB=PC=2,AP=BP=
已知四棱锥P-ABCD的底面为菱形,且∠ABC=60°,AB=PC=2,AP=BP= 已知A、B、C、D四点不共面,M、N分别是△ABD和△BCD的重心.求证:MN∥平面ACD.
已知A、B、C、D四点不共面,M、N分别是△ABD和△BCD的重心.求证:MN∥平面ACD.