题目内容

已知向量
a
=（1，2），
b
={-3，-1}，
c
=
a
+λ
b
且
a
⊥
c
，则实数λ的值为（　　）
A、-2B、-1C、1D、2
考点：数量积判断两个平面向量的垂直关系
专题：平面向量及应用
分析：由题意易得
c
的坐标，由向量垂直可得向量的数量积为0，解关于λ的方程即可．
解答： 解：∵
a
=（1，2），
b
={-3，-1}，
∴
c
=
a
+λ
b
=（1-3λ，2-λ）
∵
a
⊥
c
，∴
a
•
c
=0，
∴1×（1-3λ）+2（2-λ）=0，
解得λ=1
故选：C
点评：本题考查数量积与向量的垂直，属基础题．
练习册系列答案
相关题目
若
a
=（2，-1，3），
b
=（-4，2，x）且
a
⊥
b
，则x=
 
．
已知实数a≥1，b≥1，且a+b=4，若存在实数c使得ab+
1
ab
≥c成立，则实数c的取值范围是
 
．
给定三个向量
V1
=（1，0，1），
V2
=（1，1，0），
V3
=（0，1，k2+k-3），其中K是一个正实数，若存在非零向量同时垂直这三个向量，则K的取值为
 
．
正实数a，b满足a+2b=30，则ab的最大值为（　　）
A、
225
2
B、
125
2
C、
225
4
D、
125
4
已知集合M={0，1，2}，N={x|x⊆M}，则M与N的关系正确的是（　　）
A、M∈NB、M⊆N
C、N⊆MD、M=N
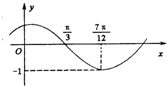函数f（x）=Asin（ωx+φ）（其中A＞0，|φ|＜
π
2
）的图象如图所示，为了得到g（x）=sin2x的图象，则只要将f（x）的图象（　　）
A、向右平移
π
6
个单位长度
B、向右平移
π
12
个单位长度
C、向左平移
π
2
个单位长度
D、向左平移
π
12
个单位长度
已知，函数f（x）的定义域为（a，b），若“?x0∈（a，b），f（x0）+f（-x0）≠0”是假命题，则f（a+b）=
 
．
已知空间向量
a
=（2，-6，c），
b
=（1，-3，2），若
a
∥
b
，则c=（　　）
A、4
B、0
C、
1
2
D、
3
2

违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com

精英家教网