题目内容
9．若函数f（x）满足f（x）+2f（$\frac{1}{x}$）=3x，则f（2）的值为（ ）| A． | -1 | B． | 2 | C． | 3 | D． | $\frac{1}{2}$ |
分析 由已知中函数f（x）满足f（x）+2f（$\frac{1}{x}$）=3x，分别令x=2，x=$\frac{1}{2}$构造方程组，解得答案．
解答 解：∵函数f（x）满足f（x）+2f（$\frac{1}{x}$）=3x，
当x=2时，f（2）+2f（$\frac{1}{2}$）=6，
当x=$\frac{1}{2}$时，f（$\frac{1}{2}$）+2f（2）=$\frac{3}{2}$，
解得：f（2）=-1，
故选：A．
点评 本题考查的知识点是抽象函数及其应用，函数求值，难度中档．
练习册系列答案
相关题目
19．偶函数f（x）（x∈R）满足：f（-4）=f（2）=0，且在区间[0，3]与[3，+∞）上分别递减和递增，则不等式x•f（x）＜0的解集为（ ）
| A． | （-∞，-4）∪（4，+∞） | B． | （-∞，-4）∪（-2，0）∪（2，4） | C． | （-∞，-4）∪（-2，0） | D． | （-4，-2）∪（2，4） |
4．已知函数f（x）=$\frac{x+1}{{x}^{2}}$，g（x）=log2x+m，若对?x1∈[1，2]，?x2∈[1，4]，使得f（x1）≥g（x2），则m的取值范围是（ ）
| A． | m≤-$\frac{5}{4}$ | B． | m≤2 | C． | m≤$\frac{3}{4}$ | D． | m≤0 |
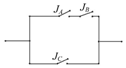如图，JA，JB两个开关串联再与开关JC并联，在某段时间内每个开关能够闭合的概率都是0.5，计算在这段时间内线路正常工作的概率为0.625．