题目内容
设函数f(x)在定义域内可导，y=f (x)的图象如图1所示，则导函数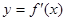
的图象可能为（ ）
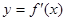的图象可能为（ ）
|
D
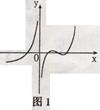
从f(x)的图像可看出f(x)在
上是增函数，
,并且增的速度越来越快.再结合x>0的图像可看出，导数值先正后负再正.所以应选D.
上是增函数，,并且增的速度越来越快.再结合x>0的图像可看出，导数值先正后负再正.所以应选D.
练习册系列答案
阳光课堂课时作业系列答案
相关题目
阳光课堂课时作业系列答案题目内容
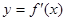的图象可能为（ ）
|
上是增函数，,并且增的速度越来越快.再结合x>0的图像可看出，导数值先正后负再正.所以应选D.阳光课堂课时作业系列答案
满足
, 且对于任意
恒有
成立。
的值；
若存在实数
，当
时，
恒成立，求实数
的最大值。
在
与
处都取得极值．
的解析式；
其中
为自然对数的底数， 
.(Ⅰ)设
，求函数
的最值；（Ⅱ）若对于任意的
，都有
成立，求
的取值范围.
上既有极大值又有极小值，则
的取值范围为
是
的导函数，
时，f (x)=x+sinx,设a=f (1),b=f (2),c=f (3),则（ ）
在
上存在单调递增区间，求
的取值范围；
时，
的最小值为
，求
在点（0,1）处的切线方程为 ▲ ．