题目内容
设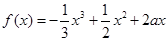
(1)若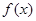 在
在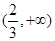 上存在单调递增区间,求
上存在单调递增区间,求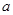 的取值范围;
的取值范围;
(Ⅱ)当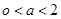 时,
时,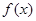 在
在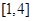 的最小值为
的最小值为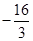 ,求
,求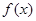 在该区间上的最大值
在该区间上的最大值
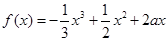
(1)若
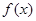 在
在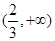 上存在单调递增区间,求
上存在单调递增区间,求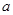 的取值范围;
的取值范围;(Ⅱ)当
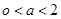 时,
时,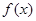 在
在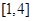 的最小值为
的最小值为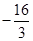 ,求
,求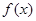 在该区间上的最大值
在该区间上的最大值(Ⅰ)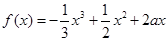 的导函数为
的导函数为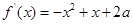 ,
,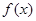 在
在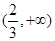 上存在单调递增区间,导函数在
上存在单调递增区间,导函数在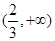 有函数值为正,
有函数值为正,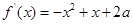 的开口向下,对称轴x=0.5,所以有
的开口向下,对称轴x=0.5,所以有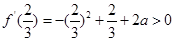 ,得
,得
(Ⅱ)因为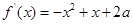 ,
, ,
, ,
, 在(1,4)内有一个零点,记为
在(1,4)内有一个零点,记为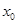 ,
,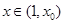 ,原函数为增函数,
,原函数为增函数, ,原函数为减函数,
,原函数为减函数,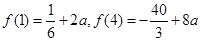 比较
比较 ,最小值为
,最小值为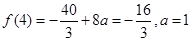 ,
,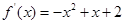 ,
, ,
,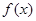 在该区间上的最大值
在该区间上的最大值

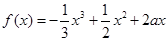 的导函数为
的导函数为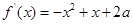 ,
,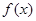 在
在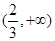 上存在单调递增区间,导函数在
上存在单调递增区间,导函数在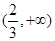 有函数值为正,
有函数值为正,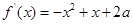 的开口向下,对称轴x=0.5,所以有
的开口向下,对称轴x=0.5,所以有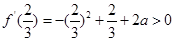 ,得
,得
(Ⅱ)因为
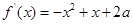 ,
, ,
, ,
, 在(1,4)内有一个零点,记为
在(1,4)内有一个零点,记为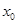 ,
,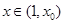 ,原函数为增函数,
,原函数为增函数, ,原函数为减函数,
,原函数为减函数,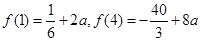 比较
比较 ,最小值为
,最小值为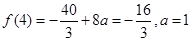 ,
,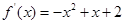 ,
, ,
,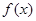 在该区间上的最大值
在该区间上的最大值

(Ⅰ)函数存在单调增区间,导函数在这个区间内内函数值有正,根据二次函数图像性质解决问题;(Ⅱ)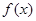 在
在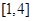 的最小值为
的最小值为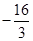 ,判断x取什么值时是最小值,求出a,然后求最大值。
,判断x取什么值时是最小值,求出a,然后求最大值。
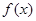 在
在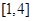 的最小值为
的最小值为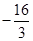 ,判断x取什么值时是最小值,求出a,然后求最大值。
,判断x取什么值时是最小值,求出a,然后求最大值。
练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
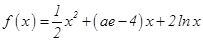 ,
, (其中
(其中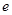 为自然对数的底数,常数
为自然对数的底数,常数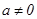 ).
).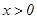 ,
,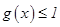 恒成立,求正实数
恒成立,求正实数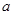 的取值范围;
的取值范围;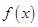 在区间
在区间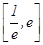 上的单调性;
上的单调性;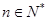 ,不等式
,不等式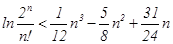 成立.
成立. 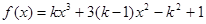 在区间(0,4)上是减函数,则
在区间(0,4)上是减函数,则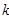 的取值范围是 ( )
的取值范围是 ( ) 



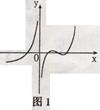
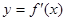 的图象可能为( )
的图象可能为( )
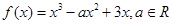
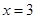 是
是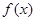 的极值点,求
的极值点,求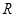 上的单调递增函数,求实数
上的单调递增函数,求实数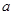 的取值范围.
的取值范围.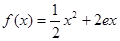 ,
,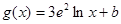 (其中
(其中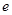 为常数,
为常数,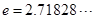 ),若这两个函数的图象有公共点,且在该点处的切线相同。
),若这两个函数的图象有公共点,且在该点处的切线相同。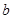 的值;
的值;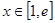 时,
时, 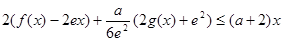 恒成立,求实数
恒成立,求实数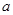 的取值范围.
的取值范围.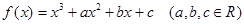 ,若函数
,若函数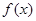 在区间
在区间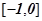 上是单调减函数,则
上是单调减函数,则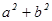 的最小值为
的最小值为
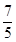


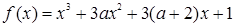 既有极大值又有极小值,则实数
既有极大值又有极小值,则实数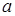 的取值范围是 。
的取值范围是 。