题目内容
已知数列{an}的各项均为正数的等比数列,且a1a2=2,a3a4=32,
(1)求数列{an}的通项公式;
(2)设数列{bn}的前n项和为Sn=n2,(n∈N*),求数列{anbn}的前n项和Tn.
(1) (2)
(2)
解析试题分析:(1)由已知条件和等比数列的通项公式列出关于q和a1的方程组,解出q和a1即可.
(2)根据bn=Sn-Sn-1,求出数列{bn}的通项公式bn的表达式,然后根据错位相减法求出数列{anbn}的前n项和Tn.
试题解析:(1)设等比数列 的公比为
的公比为 ,由已知得
,由已知得 2分
2分
又∵ ,
, ,解得
,解得 ∴
∴ ;
;
(2)由 得,
得, ,
,
∴当 时,
时, ,当
,当 时,
时, 符合上式,∴
符合上式,∴ ,(
,( )∴
)∴ ,
, ,
, , 10分
, 10分
两式相减得 ,
,
∴ . 12分
. 12分
考点:1.等比数列的通项公式;2.数列前n项和的求法.

练习册系列答案
 口算小状元口算速算天天练系列答案
口算小状元口算速算天天练系列答案
相关题目
 的前
的前 项和为
项和为 ,已知
,已知 (
( ,
, 为常数),
为常数), ,
, ,(1)求数列
,(1)求数列 成立的正整数
成立的正整数 ,
, 成等比数列, 公比为
成等比数列, 公比为 , 求证:
, 求证: .
. ,定义
,定义 它的第
它的第 项为
项为
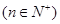 ,假设
,假设 是首项是
是首项是 公比为
公比为 的等比数列.
的等比数列. 的前
的前 ;
; ,
, ,
, .
. ;
; .
. 的前
的前 项和为
项和为 ,且
,且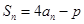 ,其中
,其中 是不为零的常数.
是不为零的常数. 时,数列
时,数列 满足
满足 ,
, ,求数列
,求数列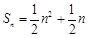 ,
, ,求数列{bn}前n项的和Tn.
,求数列{bn}前n项的和Tn. 的前n项和为
的前n项和为 ,已知
,已知 ,
,
 ,
, ,数列
,数列 的前n项和为
的前n项和为 ,
, ,证明:
,证明: .
.