题目内容
对任意实数列 ,定义
,定义 它的第
它的第 项为
项为
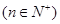 ,假设
,假设 是首项是
是首项是 公比为
公比为 的等比数列.
的等比数列.
(1)求数列 的前
的前 项和
项和 ;
;
(2)若 ,
, ,
, .
.
①求实数列 的通项
的通项 ;
;
②证明: .
.
(1) ;(2)①
;(2)① ;②详见解析.
;②详见解析.
解析试题分析:本题以新定义的模式考察了等比数列的通项公式和前n项和以及不等式的放缩法.(1)由 是首项是
是首项是 公比为
公比为 的等比数列,故实数列
的等比数列,故实数列 确定,即
确定,即
 ,再结合
,再结合 的定义,得
的定义,得 ,然后求和即可(需分类讨论);(2)由
,然后求和即可(需分类讨论);(2)由 ,
, .,可确定
.,可确定 ,利用累加法可求
,利用累加法可求 ;和式
;和式 可看作数列
可看作数列 的前n项和,故先求其通项公式,得
的前n项和,故先求其通项公式,得 ,因前n项和不易直接求出,故可考虑放缩法,首先看不等式右边,可想到证明每项都小于
,因前n项和不易直接求出,故可考虑放缩法,首先看不等式右边,可想到证明每项都小于 ,由
,由 ,进而可证明右面不等式,再考虑不等式左边,
,进而可证明右面不等式,再考虑不等式左边, ,因为
,因为
 ,故
,故 ,进而求和可证明.
,进而求和可证明.
试题解析:(1)令 这里
这里

 是公比为
是公比为 的等比数列.
的等比数列.


 ,
,
当 时,
时, ,
,
 ,. 2分
,. 2分
当 时,
时, 是公比为
是公比为 ,首项为
,首项为 的等比数列;.
的等比数列;. . 4分
. 4分 综上
综上
 . 6分
. 6分
(2)①由题设 ,
,
 ,
,
 叠加可得
叠加可得 (
( ). 8分
). 8分
②


 . 10分
. 10分
又

 ,
, ,
,
即 ,
,
 ,
,


 . 12分
. 12分

即 . 13分
. 13分
考点:1、等比数列通项公式;2、等比数列前n项和;3、累加法.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
 的前n项和
的前n项和 与通项
与通项 满足
满足 .
. ,求
,求 ;
; ,求
,求 的前n项和
的前n项和 .
. 前
前 项和
项和 .
.
 的前
的前 项和为
项和为 满足
满足 .
. 的前
的前 .
. 在点
在点 处的切线与
处的切线与 轴的交点坐标为
轴的交点坐标为 .
.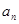 的表达式;
的表达式; ,求数列
,求数列 的前
的前 项和
项和
 的前
的前 项和
项和 满足:
满足: (
( 为常数,
为常数,
 的通项公式;
的通项公式; ,若数列
,若数列 为等比数列,求
为等比数列,求