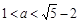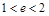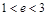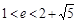题目内容
.已知直线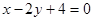 经过椭圆
经过椭圆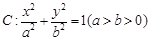 的左顶点A和上顶点D,椭圆C的右顶点为B,点P是椭圆C上位于
的左顶点A和上顶点D,椭圆C的右顶点为B,点P是椭圆C上位于 轴上方的动点,直线AP,BP与直线
轴上方的动点,直线AP,BP与直线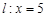 分别交于M,N两点.
分别交于M,N两点.
(1)求椭圆C的方程;
(2)求线段MN的长度的最小值;
(3)当线段MN的长度最小时,Q点在椭圆上运动,记△BPQ的面积为S,当S在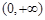 上变化时,讨论S的大小与Q点的个数之间的关系.
上变化时,讨论S的大小与Q点的个数之间的关系.
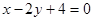 经过椭圆
经过椭圆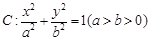 的左顶点A和上顶点D,椭圆C的右顶点为B,点P是椭圆C上位于
的左顶点A和上顶点D,椭圆C的右顶点为B,点P是椭圆C上位于 轴上方的动点,直线AP,BP与直线
轴上方的动点,直线AP,BP与直线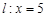 分别交于M,N两点.
分别交于M,N两点.(1)求椭圆C的方程;
(2)求线段MN的长度的最小值;
(3)当线段MN的长度最小时,Q点在椭圆上运动,记△BPQ的面积为S,当S在
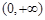 上变化时,讨论S的大小与Q点的个数之间的关系.
上变化时,讨论S的大小与Q点的个数之间的关系.解:
(1)由已知得椭圆C的左顶点为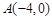 ,上顶点为D(0,2),∴
,上顶点为D(0,2),∴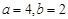 ,故椭圆C的方程为
,故椭圆C的方程为 .
.
(2)直线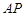 的斜率
的斜率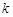 显然存在,且
显然存在,且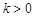 ,故可设直线AP的方程为
,故可设直线AP的方程为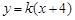 ,从而
,从而
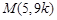 ,设
,设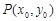 ,则
,则 ,∴直线
,∴直线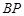 的方程为:
的方程为: ,得
,得
∴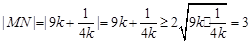
当且仅当 即
即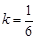 时等号成立
时等号成立
∴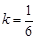 时,线段MN的长度取最小值3.
时,线段MN的长度取最小值3.
(3)由(2)知,当线段MN的长度取最小值时,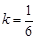 ,此时直线BP的方程为
,此时直线BP的方程为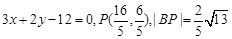
设与BP平行的直线
联立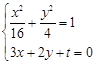 得
得
由△=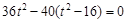 得
得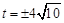
当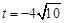 时,BP与
时,BP与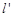 的距离为
的距离为 ,此时S△BPQ=
,此时S△BPQ=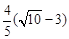
当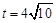 时,BP与
时,BP与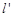 的距离为
的距离为 ,此时S△BPQ=
,此时S△BPQ=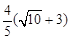
∴当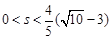 时,这样的Q点有4个
时,这样的Q点有4个
当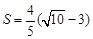 时,这样的Q点有3个
时,这样的Q点有3个
当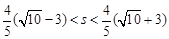 时,这样的Q点有2个
时,这样的Q点有2个
当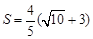 时,这样的Q点有1个
时,这样的Q点有1个
当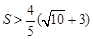 时,这样的Q点不存在.
时,这样的Q点不存在.
(1)由已知得椭圆C的左顶点为
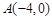 ,上顶点为D(0,2),∴
,上顶点为D(0,2),∴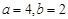 ,故椭圆C的方程为
,故椭圆C的方程为 .
. (2)直线
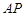 的斜率
的斜率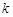 显然存在,且
显然存在,且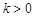 ,故可设直线AP的方程为
,故可设直线AP的方程为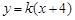 ,从而
,从而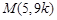 ,设
,设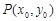 ,则
,则 ,∴直线
,∴直线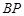 的方程为:
的方程为: ,得
,得
∴
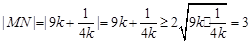
当且仅当
 即
即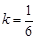 时等号成立
时等号成立∴
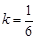 时,线段MN的长度取最小值3.
时,线段MN的长度取最小值3. (3)由(2)知,当线段MN的长度取最小值时,
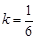 ,此时直线BP的方程为
,此时直线BP的方程为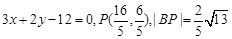
设与BP平行的直线

联立
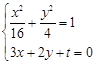 得
得
由△=
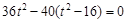 得
得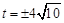
当
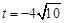 时,BP与
时,BP与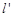 的距离为
的距离为 ,此时S△BPQ=
,此时S△BPQ=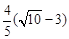
当
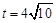 时,BP与
时,BP与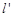 的距离为
的距离为 ,此时S△BPQ=
,此时S△BPQ=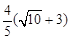
∴当
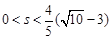 时,这样的Q点有4个
时,这样的Q点有4个当
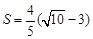 时,这样的Q点有3个
时,这样的Q点有3个当
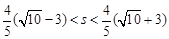 时,这样的Q点有2个
时,这样的Q点有2个当
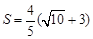 时,这样的Q点有1个
时,这样的Q点有1个当
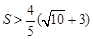 时,这样的Q点不存在.
时,这样的Q点不存在.略

练习册系列答案
相关题目
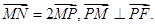
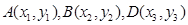 是曲线C上的点,且
是曲线C上的点,且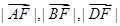 成等差数列,当AD的垂直平分线与x轴交于点E(3,0)时,求点B的坐标。
成等差数列,当AD的垂直平分线与x轴交于点E(3,0)时,求点B的坐标。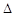 ABC内(含边界)一动点,且到三个侧面PAB,PBC,PCA的距离成等差数列,则点M的轨迹是( )
ABC内(含边界)一动点,且到三个侧面PAB,PBC,PCA的距离成等差数列,则点M的轨迹是( )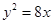 的焦点到双曲线
的焦点到双曲线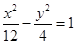 的渐近线的距离为( )
的渐近线的距离为( )

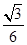
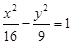 上,点Q在曲线C2:(x-5)2+y2=1上,点R在曲线C3:(x+5)2+y2=1上,则 | PQ |-| PR | 的最大值是
上,点Q在曲线C2:(x-5)2+y2=1上,点R在曲线C3:(x+5)2+y2=1上,则 | PQ |-| PR | 的最大值是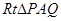 中,点
中,点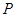 的坐标为
的坐标为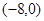 ,点
,点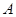 在
在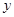 轴上,点
轴上,点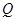 在
在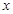 轴的正半轴上,
轴的正半轴上,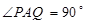 ,在
,在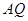 的延长线上取一点
的延长线上取一点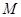 ,使
,使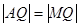 .
.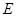 ;
;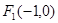 引直线与轨迹
引直线与轨迹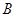 、
、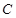 ,点
,点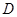 ,设
,设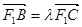 ,点
,点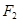 的坐标为
的坐标为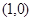 .
.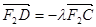 ;
;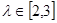 ,求
,求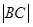 的取值范围.
的取值范围.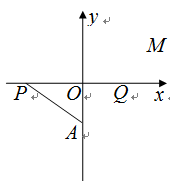
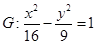 的焦点为顶点,以双曲线G的顶点为焦点作椭圆C。
的焦点为顶点,以双曲线G的顶点为焦点作椭圆C。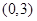 ,在y轴上是否存在定点M,过点M且斜率为k的动直线
,在y轴上是否存在定点M,过点M且斜率为k的动直线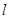 交椭圆于A、B两点,使以AB为直径的圆恒过点P,若存在,求出M的坐标;若不存在,说明理由。
交椭圆于A、B两点,使以AB为直径的圆恒过点P,若存在,求出M的坐标;若不存在,说明理由。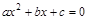 无实根,则双曲线离心率的取值范围是( )
无实根,则双曲线离心率的取值范围是( )