题目内容
(本小题共14分)
已知椭圆![]() 的焦点在
的焦点在![]() 轴上,离心率为
轴上,离心率为![]() ,对称轴为坐标轴,且经过点
,对称轴为坐标轴,且经过点![]() .
.
(Ⅰ)求椭圆![]() 的方程;
的方程;
(Ⅱ)直线![]() 与椭圆
与椭圆![]() 相交于A,B两点,在
相交于A,B两点,在![]() 上存在一点
上存在一点![]() ,
,![]() 上存在一点
上存在一点![]() ,使得
,使得![]() ,若原点
,若原点![]() 在以
在以![]() 为直径的圆上,求直线斜率
为直径的圆上,求直线斜率![]() 的值.
的值.
(本小题共14分)
已知椭圆![]() 的焦点在
的焦点在![]() 轴上,离心率为
轴上,离心率为![]() ,对称轴为坐标轴,且经过点
,对称轴为坐标轴,且经过点![]() .
.
(Ⅰ)求椭圆![]() 的方程;
的方程;
(Ⅱ)直线![]() 与椭圆
与椭圆![]() 相交于A,B两点,在
相交于A,B两点,在![]() 上存在一点
上存在一点![]() ,
,![]() 上存在一点
上存在一点![]() ,使得
,使得![]() ,若原点
,若原点![]() 在以
在以![]() 为直径的圆上,求直线斜率
为直径的圆上,求直线斜率![]() 的值.
的值.
解:(Ⅰ) 依题意,可设椭圆![]() 的方程为
的方程为![]() . ……………………1分
. ……………………1分
∵ ![]() , ∴
, ∴ ![]() ,
,![]() . ……………………3分
. ……………………3分
∵ 椭圆经过点![]() ,
,
∴ 椭圆的方程为![]() . ……………………5分
. ……………………5分
(Ⅱ) 记![]() 两点坐标分别为
两点坐标分别为![]() ,
,![]() ,
,
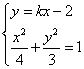 消y,得
消y,得![]() . ……………………7分
. ……………………7分
∵ 直线与椭圆有两个交点,
∴ ![]() ,
,
∴ ![]() . ……………………9分
. ……………………9分
由韦达定理 ![]() ,
,![]() .
.
∵ 原点![]() 在以
在以![]() 为直径的圆上,
为直径的圆上,
∴ ![]() ,即
,即![]() .
.
∵ ![]() ,
,![]() 在
在![]() 上,
上,![]() 在
在![]() 上
上
∴ ![]() , ……………………10分
, ……………………10分
又![]() ,
,![]() ,
,
∴ ![]()
![]()
![]()
![]() .
.
∴ ![]() , ……………………13分
, ……………………13分
∴ ![]() . ……………………14分
. ……………………14分

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目

 底面ABCD,PD=DC,点E是PC的中点,作EF
底面ABCD,PD=DC,点E是PC的中点,作EF
 的棱长为
的棱长为 ,
, 是
是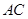 与
与 的交点,
的交点, 为
为 的中点.
的中点. ∥平面
∥平面 ;
; 平面
平面 ;
; 的体积.
的体积.