题目内容

设
e1
，
e2
是两个不共线的向量
（1）已知
AB
=2
e1
+k
e2
，
CB
=
e1
+3
e2
，
CD
=2
e1
-
e2
，若A，B，D三点共线，求k的值
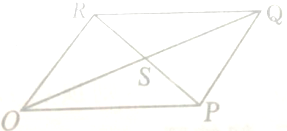
（2）如图，在平行四边形OPQR中，S是对角线的交点，若
OP
=2
e1
，
OR
=3
e2
，以
e1
，
e2
为基底表示
PS
与
QS
．
考点：平面向量的基本定理及其意义
专题：平面向量及应用
分析：（1）由
CB
=
e1
+3
e2
，
CD
=2
e1
-
e2
，可得
BD
=
CD
-
CB
=
e1
-4
e2
，由A，B，D三点共线，可得存在实数λ使得
AB
=λ
BD
，展开利用向量基本定理即可得出．
（2）利用向量共线定理、向量的平行四边形法则即可得出．
解答： 解：（1）∵
CB
=
e1
+3
e2
，
CD
=2
e1
-
e2
，
∴
BD
=
CD
-
CB
=
e1
-4
e2
，
∵A，B，D三点共线，
∴存在实数λ使得
AB
=λ
BD
，
∴2
e1
+k
e2
=λ(
e1
-4
e2
)=λ
e1
-4λ
e2
，
∵
e1
，
e2
是两个不共线的向量，
∴
2=λ
k=-4λ
，解得k=-8．
（2）
PS
=
1
2
PR
=
1
2
(
OR
-
OP
)=
1
2
(3
e2
-2
e1
)，
QS
=-
1
2
OQ
=-
1
2
(
OP
+
OR
)=-
1
2
(2
e1
+3
e2
)．
点评：本题考查了向量基本定理、向量共线定理、向量的平行四边形法则，考查了计算能力，属于基础题．
练习册系列答案
相关题目
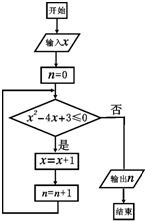在区间[-2，3]上随机选取一个数M，不变执行如图所示的程序框图，且输入x的值为1，然后输出n的值为N，则M≤N-2的概率为（　　）
A、
1
5
B、
2
5
C、
3
5
D、
4
5
已知函数f（x）=
5
2
sinAsinx+cos2x（x∈R），其中A、B、C是△ABC的三个内角，且满足cos（A+
π
4
）=-
2
10
，A∈（
π
4
，
π
2
）
（1）求sinA的值；
（2）若f（B）=
3
2
，且AC=5，求BC的值．
已知sinx+2cosy=2，求cosx+2siny的范围．
已知a，b∈{-1，1，2}，则直线ax+by-3=0（a2+b2≠0）与圆x2+y2=4有公共点的概率是
 
．
函数f（x）=ln（x+1）-
2
x
的零点所在的区间是（n，n+1），则正整数n=
 
．
已知向量
a
=（λ，1），
b
=（λ+2，1），若|
a
+
b
|=|
a
-
b
|，则实数λ的值为（　　）
A、1B、2C、-1D、-2
设A、B是双曲线
x2
a2
-
y2
b2
=1（a＞0，b＞0）的左、右顶点，F是右焦点，M是双曲线上异于A、B的动点，过点B作x轴的垂线与直线MA交于点P．若直线OP与BM的斜率之积为4，则双曲线的离心率为
 
．
已知函数f（x）=[x]，符号[x]表示不超过x的最大整数，求f（x2+
1
2
）=2x-1的解集．

违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com

精英家教网