Question

【题目】已知点是椭圆C：上的一点，椭圆C的离心率与双曲线的离心率互为倒数，斜率为直线l交椭圆C于B，D两点，且A、B、D三点互不重合．

（1）求椭圆C的方程；

（2）若分别为直线AB，AD的斜率，求证：为定值。

Answer 1

【答案】（1）（2）详见解析

【解析】

（1）根据椭圆的定义和几何性质，建立方程，即可求椭圆C的方程；

（2）设直线BD的方程为，代入椭圆方程，设D（x1，y1），B（x2，y2），直线AB、AD的斜率分别为：，则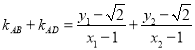，由此导出结果.

（1）由题意，可得e==，代入A（1，）得，

又，解得，

所以椭圆C的方程．

（2）证明：设直线BD的方程为y=x+m，

又A、B、D三点不重合，∴，

设D（x1，y1），B（x2，y2），

则由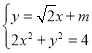得4x2+2mx+m2-4=0

所以△=-8m2+64＞0，所以＜m＜．

x1+x2=-m，

设直线AB、AD的斜率分别为：kAB、kAD，

则kAD+kAB=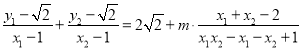

=

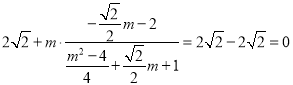
所以kAD+kAB=0，即直线AB，AD的斜率之和为定值．