题目内容
平面向量
=(1,2),
=(-4,2),
=m
+
(m∈R).
(1)若
⊥
,求m的值;
(2)若
与
的夹角等于
与
的夹角,求|
|的值.
| a |
| b |
| c |
| a |
| b |
(1)若
| a |
| c |
(2)若
| c |
| a |
| c |
| b |
| c |
考点:平面向量数量积的运算,平面向量数量积的坐标表示、模、夹角
专题:平面向量及应用
分析:(1)利用向量垂直与数量积的关系即可得出;
(2)利用向量的夹角公式和数量积运算即可得出.
(2)利用向量的夹角公式和数量积运算即可得出.
解答:
解:(1)∵
⊥
,
=m
+
(m∈R).
∴
•
=
•(m
+
)=m
2+
•
=m×(
)2-4+4=0,
解得m=0.
(2)
•
=
•(m
+
)=m
•
+
2=m(-4+4)+(16+4)=20.
∵
与
的夹角等于
与
的夹角,∴cos<
,
>=cos<
,
>,
∴
=
,
∴
=
,解得m=2.∴
=2
+
=2(1,2)+(-4,2)=(-2,6).
∴|
|=
=2
.
| a |
| c |
| c |
| a |
| b |
∴
| a |
| c |
| a |
| a |
| b |
| a |
| a |
| b |
| 5 |
解得m=0.
(2)
| b |
| c |
| b |
| a |
| b |
| a |
| b |
| b |
∵
| c |
| a |
| c |
| b |
| a |
| c |
| c |
| b |
∴
| ||||
|
|
| ||||
|
|
∴
| 5m | ||
|
| 20 | ||
|
| c |
| a |
| b |
∴|
| c |
| (-2)2+62 |
| 10 |
点评:本题考查了向量垂直与数量积的关系、向量的夹角公式和数量积运算,属于基础题.

练习册系列答案
相关题目
用反证法证明某命题时,对结论:“自然数a,b,c都是偶数”,正确的反设为( )
| A、a,b,c中至少有一个是奇数 |
| B、a,b,c中至多有一个是奇数 |
| C、a,b,c都是奇数 |
| D、a,b,c中恰有一个是奇数 |
在平面直角坐标系中,以点(1,1)为圆心,以
为半径的圆在以直角坐标系的原点为极点,以ox轴为极轴的极坐标系中对应的极坐标方程为( )
| 2 |
A、ρ=2
| ||||
B、ρ=2
| ||||
C、ρ=2
| ||||
D、ρ=2
|
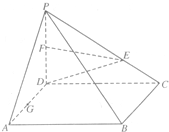 如图,ABCD是正方形,PD⊥底面ABCD,点E在PC上,F,G分别是PD和AD的中点.
如图,ABCD是正方形,PD⊥底面ABCD,点E在PC上,F,G分别是PD和AD的中点.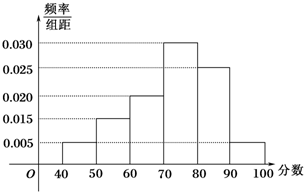 从参加高一年级某次模块考试中抽出80名学生,其数学成绩(均为整数)的频率分布直方图如图所示.
从参加高一年级某次模块考试中抽出80名学生,其数学成绩(均为整数)的频率分布直方图如图所示.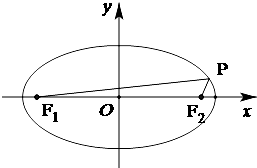 已知椭圆
已知椭圆