题目内容
在正三棱柱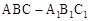 中,若AB=2,
中,若AB=2,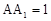 则点A到平面
则点A到平面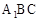 的距离为( )
的距离为( )
A.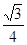 | B. | C.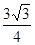 | D. |
B
解析试题分析:取BC中点D,连接 ,过A作
,过A作
 面
面 ,
, 面
面 ,所求距离为AE,因为AB=2,
,所求距离为AE,因为AB=2,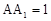

 ,所求距离为
,所求距离为
考点:点到面的距离
点评:求点到面的距离常用方法有:做垂线段,求垂线段长度;等体积法求三棱锥的高;向量法利用坐标代入公式计算

练习册系列答案
相关题目
长方体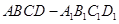 中,
中, 则
则 所成的角的大小是
所成的角的大小是
A. | B. | C. | D. |
下列命题中,m、n表示两条不同的直线,α、β、γ表
示三个不同的平面.
①若m⊥α,n∥α,则m⊥n;
②若α⊥γ,β⊥γ,则α∥β;
③若m∥α,n∥α,则m∥n;
④若α∥β,β∥γ,m⊥α,则m⊥γ.
则正确的命题是
| A.①③ | B.②③ | C.①④ | D.②④ |
如图,面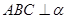 ,
,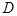 为
为 的中点,
的中点,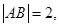
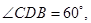
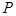 为面
为面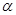 内的动点,且
内的动点,且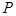 到直线
到直线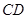 的距离为
的距离为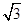 ,则
,则 的最大值( )
的最大值( )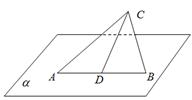
A. | B. | C. | D.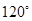 |
如图,在正四棱柱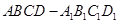 中,
中,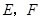 分别是
分别是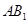 ,
,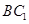 的中点,则以下结论中不成立的是( )
的中点,则以下结论中不成立的是( )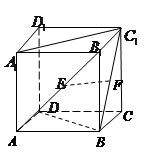
A.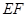 与 与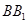 垂直 垂直 | B.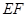 与 与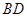 垂直 垂直 |
C.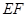 与 与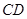 异面 异面 | D.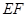 与 与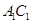 异面 异面 |

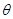 ,现沿对角线BD折成60°的二面角,翻折后
,现沿对角线BD折成60°的二面角,翻折后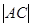 =
= a,则锐角A是( )
a,则锐角A是( )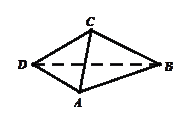

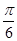


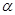 、
、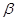 .下列四个命题中,
.下列四个命题中,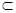
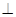
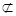
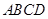 沿对角线
沿对角线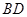 折成直二面角
折成直二面角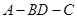 ,有如下四个结论:
,有如下四个结论: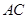 ⊥
⊥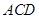 是等边三角形;
是等边三角形;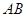 与平面
与平面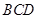 所成的角为60°; ④
所成的角为60°; ④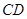 所成的角为60°.
所成的角为60°.