题目内容
设b>0,数列{an}满足a1=b,an= (n≥2)。
(n≥2)。
(1)求数列{an}的通项公式;
(2)证明:对于一切正整数n,an≤ +1。
+1。
 (n≥2)。
(n≥2)。(1)求数列{an}的通项公式;
(2)证明:对于一切正整数n,an≤
 +1。
+1。解:(1) ,得
,得
设 ,则
,则

(i)当 时,
时, 是以
是以 为首项,
为首项, 为公差的等差数列
为公差的等差数列
即
∴ ;
;
(ii)当 时,设
时,设
则
令 ,得
,得
∴

知 是等比数列
是等比数列
∴
又
∴
∴ ;
;
(2)(i)当 时,
时, ,故
,故 时,命题成立;
时,命题成立;
(ii)当 时,
时,
 ,…,
,…,
以上n个式子相加得







故当 时,命题成立
时,命题成立
综上(i)(ii)知命题成立。
 ,得
,得
设
 ,则
,则

(i)当
 时,
时, 是以
是以 为首项,
为首项, 为公差的等差数列
为公差的等差数列即

∴
 ;
;(ii)当
 时,设
时,设
则

令
 ,得
,得
∴


知
 是等比数列
是等比数列∴

又

∴

∴
 ;
;(2)(i)当
 时,
时, ,故
,故 时,命题成立;
时,命题成立;(ii)当
 时,
时,
 ,…,
,…,
以上n个式子相加得








故当
 时,命题成立
时,命题成立综上(i)(ii)知命题成立。

练习册系列答案
相关题目
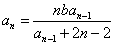 (n≥2)。
(n≥2)。