题目内容
已知函数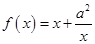 ,
,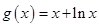 ,其中
,其中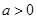 .
.
(1)若 是函数
是函数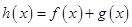 的极值点,求实数
的极值点,求实数 的值;
的值;
(2)若对任意的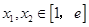 (
(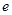 为自然对数的底数)都有
为自然对数的底数)都有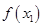 ≥
≥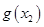 成立,求实数
成立,求实数 的取值范围.
的取值范围.
(1)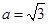 (2)
(2)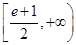
解析试题分析:解:∵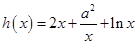 ,其定义域为
,其定义域为 ,
,
∴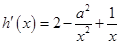 .
.
∵ 是函数
是函数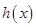 的极值点,∴
的极值点,∴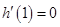 ,
,
即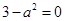 .
.
∵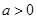 ,∴
,∴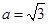 .
.
(2) 对任意的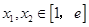 都有
都有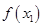 ≥
≥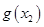 成立等价于对任意的
成立等价于对任意的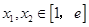
都有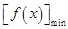 ≥
≥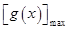 .
.
当
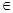 [1,
[1,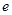 ]时,
]时,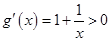 .
.
∴函数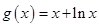 在
在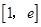 上是增函数.
上是增函数.
∴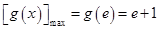 .
.
∵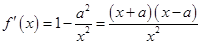 ,且
,且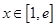 ,
,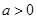 .
.
①当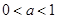 且
且
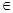 [1,
[1,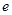 ]时,
]时,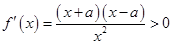 ,
,
∴函数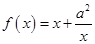 在[1,
在[1,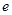 ]上是增函数,
]上是增函数,
∴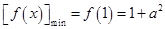 .
.
由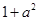 ≥
≥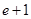 ,得
,得 ≥
≥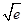 ,
,
又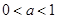 ,∴
,∴ 不合题意.
不合题意.
②当1≤ ≤
≤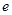 时,
时,
若1≤ <
< ,则
,则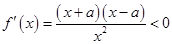 ,
,
若 <
< ≤
≤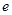 ,则
,则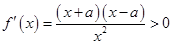 .
.
∴函数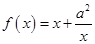 在
在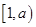 上是减函数,在
上是减函数,在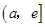 上是增函数.
上是增函数.
∴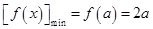 .
.
由 ≥
≥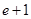 ,得
,得 ≥
≥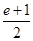 ,
,
又1≤ ≤
≤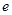 ,∴
,∴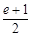 ≤
≤
练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
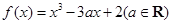 .
. 的单调递增区间;
的单调递增区间;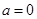 时,在曲线
时,在曲线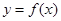 上是否存在两点
上是否存在两点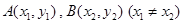 ,使得曲线在
,使得曲线在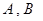 两点处的切线均与直线
两点处的切线均与直线 交于同一点?若存在,求出交点纵坐标的取值范围;若不存在,请说明理由;
交于同一点?若存在,求出交点纵坐标的取值范围;若不存在,请说明理由;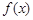 在区间
在区间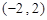 存在最大值
存在最大值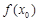 ,试构造一个函数
,试构造一个函数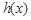 ,使得
,使得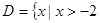 ,且
,且 ;②当
;②当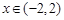 时,
时,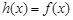 ;③在
;③在 中使
中使 值,从小到大组成等差数列.(只要写出函数
值,从小到大组成等差数列.(只要写出函数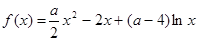 ,
, .
.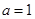 ,求函数
,求函数 的极值;
的极值;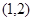 上有极值,求
上有极值,求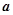 的取值范围.
的取值范围. ,请用定义证明
,请用定义证明 在
在
 上为减函数.
上为减函数.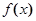 是一次函数,其图像过点
是一次函数,其图像过点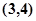 ,且
,且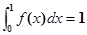 ,求
,求 ,且
,且
 ;
;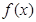 的奇偶性;
的奇偶性; 上的单调性,并证明。
上的单调性,并证明。 对定义域内任意
对定义域内任意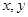 ,有
,有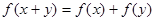
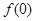 ;
;
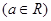 .
.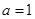 时,证明:
时,证明: 在
在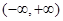 上为减函数;
上为减函数;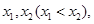 求实数
求实数 的取值范围.
的取值范围.