题目内容
．设α为第四象限的角，若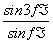
＝
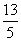，则tan 2α＝________.
－
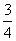
解析 由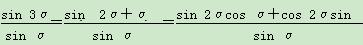
＝2cos2α＋cos 2α＝.
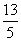∵2cos2α＋cos 2α＝1＋2cos 2α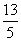＝，∴cos 2α＝
.
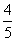∵α为第四象限角，
∴2kπ＋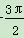
<α<2kπ＋2π，(k∈Z)
∴4kπ＋3π<2α<4kπ＋4π，(k∈Z)
故2α可能在第三、四象限，
又∵cos 2α＝，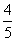
∴sin 2α＝－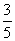
，tan 2α＝－.
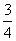练习册系列答案
相关题目
题目内容
．设α为第四象限的角，若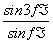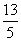＝，则tan 2α＝________.
－
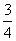
解析 由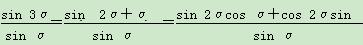＝2cos2α＋cos 2α＝.
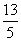∵2cos2α＋cos 2α＝1＋2cos 2α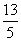＝，∴cos 2α＝.
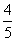∵α为第四象限角，
∴2kπ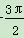＋<α<2kπ＋2π，(k∈Z)
∴4kπ＋3π<2α<4kπ＋4π，(k∈Z)
故2α可能在第三、四象限，
又∵cos 2α＝，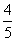
∴sin 2α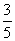＝－，tan 2α＝－.
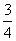)的部分图象，如图所示．
上有两个不同的实根，试求a的取值范围．
的值为( )
B.
C.
D．－2
B.
C.
D.
，0)，点P(x，y)在y＝sin x的图象上运动，点Q在y＝f(x)的图象上运动．且满足
＝m⊗
＋n(其中O为坐标原点)，则y＝f(x)的最大值A及最小正周期T分别为( )
)＋asin(x－
)的一条对称轴方程为x＝
，则a等于( )
C．2 D．3
，x∈(0,3)，则( )
B．f(x)有最小值－1