题目内容
19.已知f(x)=x2+ax+b,a,b∈R,不等式x>f(x)的解集是(-2,4),则f(x)>f(f(x))的解是(-3,-2)∪(3,4).分析 根据x2+(a-1)x+b<0的解集是(-2,4),求出a,b的值,得到f(x)的解析式,解不等式即可.
解答 解:不等式x>f(x)的解集是(-2,4),
即x2+(a-1)x+b<0的解集是(-2,4),
∴$\left\{\begin{array}{l}{-2+4=-(a-1)}\\{-2×4=b}\end{array}\right.$,解得$\left\{\begin{array}{l}{a=-1}\\{b=-8}\end{array}\right.$,
∴f(x)=x2-x-8,
∴f(x)>f(f(x))即x2-x-8>(x2-x-8)2-(x2-x-8)-8,
解得:-2<x2-x-8<4,
∴$\left\{\begin{array}{l}{{x}^{2}-x-8>-2}\\{{x}^{2}-x-8<4}\end{array}\right.$,
解得:-3<x<-2或3<x<4;
故答案为:(-3,-2)∪(3,4).
点评 本题考查了二次函数的性质,考查解不等式问题,是一道中档题.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
10.i是虚数单位,若复数z满足zi=-1+i,则复数z的实部与虚部的和是( )
| A. | 0 | B. | 1 | C. | 2 | D. | 3 |
4.已知函数f(x)=lnx的图象总在函数g(x)=ax2-$\frac{1}{2}$(a>0)图象的下方,则实数a的取值范围是( )
| A. | (0,$\frac{1}{2}$] | B. | (0,$\frac{1}{2}$) | C. | [$\frac{1}{2}$,+∞) | D. | ($\frac{1}{2}$,+∞) |
8.盒子中共有12盒奶,工商人员从中任取3盒进行质量检查,则不同抽取方法的种数是( )
| A. | 22 | B. | 48 | C. | 84 | D. | 220 |
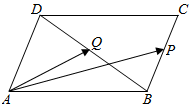 在边长为2的菱形ABCD中,∠BAD=60°,P,Q分别是BC,BD的中点,则向量$\overrightarrow{AP}$与$\overrightarrow{AQ}$的夹角的余弦值为$\frac{3\sqrt{21}}{14}$.
在边长为2的菱形ABCD中,∠BAD=60°,P,Q分别是BC,BD的中点,则向量$\overrightarrow{AP}$与$\overrightarrow{AQ}$的夹角的余弦值为$\frac{3\sqrt{21}}{14}$.