题目内容

20．已知集合A={x|${log}_{\frac{1}{2}}（x+2）＜0$}，集合B={x|（x-a）（x-b）＜0}，若“a=-3”是“A∩B≠∅”的充分条件，则实数b的取值范围是b＞-1．

分析 分别求出关于A、B的不等式，通过A∩B≠∅”，求出b的范围即可．

解答 解：A={x|${log}_{\frac{1}{2}}（x+2）＜0$}={x|x＞-1}，
B={x|（x-a）（x-b）＜0}=（-3，b）或（b，-3），
由“A∩B≠∅”，得b＞-1，
故答案为：b＞-1．

点评 本题考查了充分必要条件，考查对数函数以及解不等式问题，考查集合的关系，是一道基础题．

练习册系列答案
相关题目
12．设复数z1=-1+2i，z2=2+i，其中i为虚数单位，则z1•z2=（　　）
A．-4B．3iC．-3+4iD．-4+3i
12．已知集合A={x|（x+3）（x-1）≤0}，B={x|y=lg（x2-x-2）}，则A∩（CRB）=（　　）
A．[-3，-1）B．[-3，-1]C．[-1，1]D．（-1，1]
8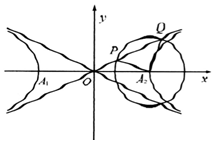．如图，已知过双曲线$\frac{x^2}{a^2}-\frac{y^2}{b^2}$=1（a＞0，b＞0）的右顶点A2作一个圆，该圆与其渐近线bx-ay=0交于点P，Q，若∠PA2Q=90°，|PQ|=2|OP|，则该双曲线的离心率为（　　）
A．$\frac{{\sqrt{7}}}{2}$B．$\frac{{\sqrt{5}}}{2}$C．$\sqrt{5}$D．$\sqrt{3}$
15．已知F1、F2分别是双曲线$\frac{{x}^{2}}{{a}^{2}}$-$\frac{{y}^{2}}{{b}^{2}}$=1的左、右焦点，过F2作x轴的垂线与双曲线交于A、B两点，G是△ABF1的重心，且$\overrightarrow{GA}$•$\overrightarrow{{F}_{1}B}$=0，则双曲线的离心率为$\sqrt{3}$．
5．已知函数f（x）=|x-a|+m|x+a|（0＜m＜1，m，a∈R），若对于任意的实数x不等式f（x）≥2恒成立时，实数a的取值范围是{a|a≤-5或a≥5}，则所有满足条件的m的组成的集合是{$\frac{1}{5}$}．
12．已知函数$f（x）=2-\frac{3}{x}$，若g（x）=f（x）-m为奇函数，则实数m的值为（　　）
A．-3B．-2C．2D．3
9．某市家庭煤气的使用量x（m3）和煤气费f（x）（元） 满足关系f（x）=$\left\{\begin{array}{l}{C，0＜x≤A}\\{C+B（x-A），x＞A}\end{array}\right.$，已知某家庭今年前三个月的煤气费如表：
月份用气量煤气费
一月份4m34 元
二月份25m314 元
三月份35m319 元
若四月份该家庭使用了20m3的煤气，则其煤气费为（　　）元．
A．10.5B．10C．11.5D．11
9．已知命题p：?x0∈（-∞，0），2x0＜3x0，命题$q：?x∈（{0，\frac{π}{2}}），sinx＜x$，则下列命题中真命题是（　　）
A．p∧qB．p∨（￢q）C．p∧（￢q）D．（￢p）∧q

违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com

精英家教网