题目内容
设函数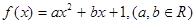 。
。
(Ⅰ)若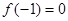 且对任意实数
且对任意实数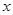 均有
均有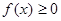 成立,求
成立,求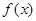 的表达式;
的表达式;
(Ⅱ)在(Ⅰ)的条件下,当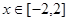 时,
时,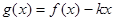 是单调函数,求实数
是单调函数,求实数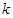 的取值范围.
的取值范围.
【答案】
(Ⅰ)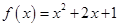 ,(Ⅱ)
,(Ⅱ)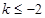 或
或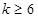
【解析】
试题分析:(Ⅰ)根据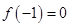 得出a,b关系,再
得出a,b关系,再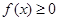 在定义域上恒成立,可得a,b的值,从而得出
在定义域上恒成立,可得a,b的值,从而得出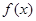 表达式.
表达式.
(Ⅱ)由(Ⅰ)可推出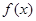 表达式,又
表达式,又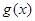 为单调函数,利用二次函数性质求得实数
为单调函数,利用二次函数性质求得实数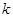 的取值范围.
的取值范围.
试题解析:(Ⅰ)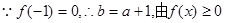 恒成立,
恒成立,
知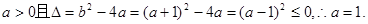
从而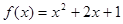 .(6分)
.(6分)
(Ⅱ)由(1)可知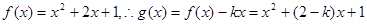 ,
,
由于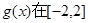 是单调函数,
是单调函数,
知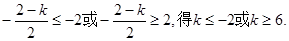 .(12分)
.(12分)
考点:二次函数求解析式,单调区间求参量.

练习册系列答案
 口算题天天练系列答案
口算题天天练系列答案
相关题目
设函数f(x)=xtanx,若 且
且 ,则下列结论中必成立的是( )
,则下列结论中必成立的是( )
A. | B. | C. | D. |
 且
且 ,则下列结论中必成立的是( )
,则下列结论中必成立的是( ) B.
B. C.
C. D.
D.