题目内容
直角坐标平面上，有2013个非零向量
、
、
、…、
，且
⊥
（k=1，2，…，2012），各向量的横坐标和纵坐标均为非负实数，若|
|+|
|+|
|+…+|
|=l（常数），则|
+
+
+…+
|的最小值为 ．
| a1 |
| a2 |
| a3 |
| a2013 |
| ak |
| ak+1 |
| a1 |
| a2 |
| a3 |
| a2013 |
| a1 |
| a2 |
| a3 |
| a2013 |
考点：向量的加法及其几何意义
专题：平面向量及应用
分析：由于2013个非零向量
、
、
、…、
，且
⊥
（k=1，2，…，2012），各向量的横坐标和纵坐标均为非负实数，不妨设图形如图所示．设
+
+…+
=
=（m，0），
+
+…+
=
=（0，n）．可得
⊥
，|
|=|
|+|
|+…+|
|=m，|
|=|
|+|
|+…+
|=n．又|
|+|
|+|
|+…+|
|=l（常数），即m+n=l，再利用均值不等式的性质即可得出．
| a1 |
| a2 |
| a3 |
| a2013 |
| ak |
| ak+1 |
| a1 |
| a3 |
| a2013 |
| OA |
| a2 |
| a4 |
| a2012 |
| OB |
| OA |
| OB |
| OA |
| a1 |
| a3 |
| a2013 |
| OB |
| a2 |
| a4 |
| |a2012 |
| a1 |
| a2 |
| a3 |
| a2013 |
解答：
解：由于2013个非零向量
、
、
、…、
，且
⊥
（k=1，2，…，2012），各向量的横坐标和纵坐标均为非负实数，不妨设图形为：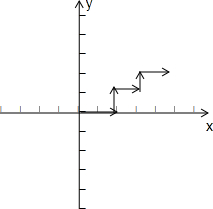
设
+
+…+
=
=（m，0）
+
+…+
=
=（0，n）．
则
⊥
，|
|=|
|+|
|+…+|
|=m，
|
|=|
|+|
|+…+
|=n．
又|
|+|
|+|
|+…+|
|=l（常数），
∴m+n=l，
∵
+
+
+…+
=
+
=（m，n），
∴|
+
+
+…+
|=|
+
|
=
≥
=
l，当且仅当|
|=|
|=
l时取等号．
∴|
+
+
+…+
|的最小值为
l．
故答案为：
l．
| a1 |
| a2 |
| a3 |
| a2013 |
| ak |
| ak+1 |
设
| a1 |
| a3 |
| a2013 |
| OA |
| a2 |
| a4 |
| a2012 |
| OB |
则
| OA |
| OB |
| OA |
| a1 |
| a3 |
| a2013 |
|
| OB |
| a2 |
| a4 |
| |a2012 |
又|
| a1 |
| a2 |
| a3 |
| a2013 |
∴m+n=l，
∵
| a1 |
| a2 |
| a3 |
| a2013 |
| OA |
| OB |
∴|
| a1 |
| a2 |
| a3 |
| a2013 |
| OA |
| OB |
=
| m2+n2 |
| m+n | ||
|
| ||
| 2 |
| OA |
| OB |
| 1 |
| 2 |
∴|
| a1 |
| a2 |
| a3 |
| a2013 |
| ||
| 2 |
故答案为：
| ||
| 2 |
点评：本题考查了向量的加法运算、数量积的性质、均值不等式等基础知识与基本技能方法，考查了推理能力和数形结合的能力，属于难题．
练习册系列答案
相关题目
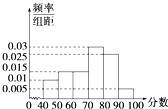某校举行了由全部学生参加的校园安全知识考试，从中抽出60名学生，将其成绩分成六段[40，50），[50，60），…，[90，100]后，画出如图所示的频率分布直方图．观察图形的信息，回答下列问题：估计这次考试的及格率（60分及以上为及格）为已知函数f（x）=
．设a=log20.8，则f（f（a））的值等于（ ）
|
| A、1 | B、2 | C、-1 | D、-2 |