题目内容
10．若集合A={x|-1≤2x+1≤3}，B={y|y=x2-2x（x∈（2，3]}，求A∩B，（∁RA）∪B．分析 化简集合A、B，根据交集、补集和并集的定义进行运算即可．
解答 解：∵集合A={x|-1≤2x+1≤3}={x|-1≤x≤1}，
B={y|y=x2-2x，x∈（2，3]}={y|0＜y≤3}，
∴A∩B={x|0＜x≤1}，
∁RA={x|x＜-1或x＞1}，
∴（∁RA）∪B={x|x＜-1或x＞0}．
点评 本题考查了集合的化简与运算问题，是基础题目．
练习册系列答案
相关题目
20．设Sn是等差数列{an}的前n项和，若$\frac{a_5}{a_3}$=2，则$\frac{S_9}{S_5}$=（ ）
| A． | $\frac{18}{5}$ | B． | $\frac{14}{5}$ | C． | $\frac{12}{5}$ | D． | $\frac{9}{5}$ |
18．下列函数中，既不是奇函数，也不是偶函数的是（ ）
| A． | y=x+sin 2x | B． | y=x2-cos x | C． | y=2x+$\frac{1}{{2}^{x}}$ | D． | y=x2+sin x |
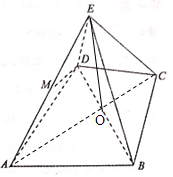如图几何体E-ABCD是四棱锥，△ABD为正三角形，∠BCD=120°，CB=CD=CE=1，AB=AD=AE=$\sqrt{3}$，且EC⊥BD，
15．已知集合M={x|-1＜x＜3，x∈R}，N={-1，0，1，2，3}，则M∩N=（ ）
| A． | {-1，0，2，3} | B． | {-1，0，1，2} | C． | {0，1，2} | D． | {0，1，2，3} |
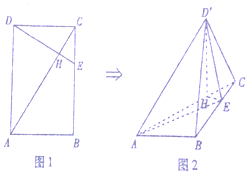如图1，已知矩形ABCD中，点E是边BC上的点，DE与AC相交于点H，且CE=1，AB=$\sqrt{3}$，BC=3，现将△ACD沿AC折起，如图2，点D的位置记为D′，此时ED′=$\frac{\sqrt{10}}{2}$